前回は、AntiVirus を支える情報検索アルゴリズム 1 として Aho–Corasick アルゴリズムの実装と ClamAV における利用方法を確認しました。
今回は、同じく ClamAV のコードをベースに、シグネチャパターンマッチング処理に応用される Boyer–Moore(BM) 法や Wu-Manber (WM) 法などについてまとめます。
もくじ
(前提) ClamAV におけるパターンマッチングの処理(再掲)
前回の記事 でも記載した通り、ClamAV におけるファイルスキャンのコア関数である cli_scan_fmap 関数は、簡単に言うと cl_fmap 構造体として抽象化されたメモリマップのスキャンを行う関数です。
この中では、ハッシュベースのチェックや、ロードされているシグネチャデータベースとのパターンマッチングなどの処理が行われます。
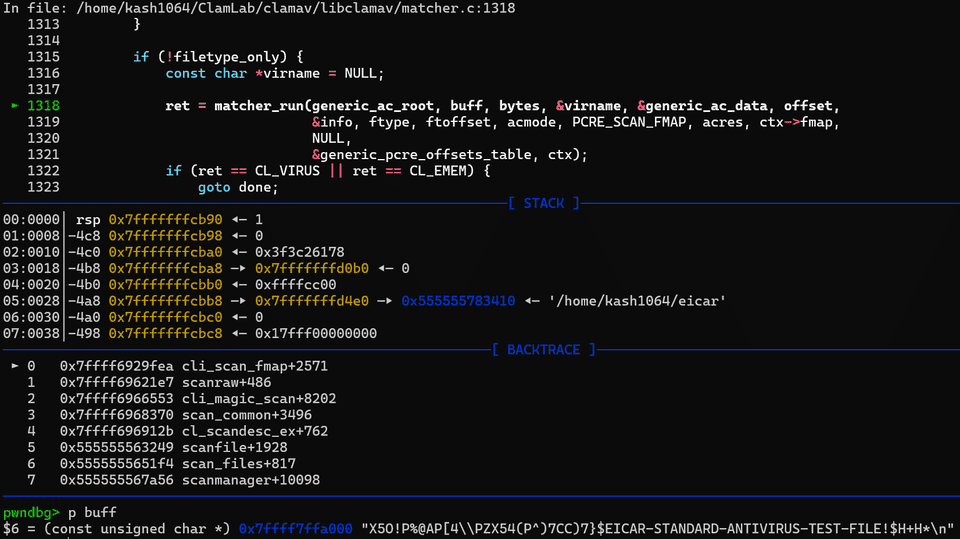
cli_scan_fmap 関数は、スキャンのための初期化を行った後にファイルマップから最大 SCANBUFF(0x20000 バイト) 分のバッファを 1 チャンクとして読み込み、 matcher_run 関数によるスキャンを行います。
この matcher_run 関数は以下のパラメーターと共に呼び出され、受け取ったバッファのスキャンを行います。
static inline cl_error_t matcher_run(
const struct cli_matcher *root,
const unsigned char *buffer, uint32_t length,
const char **virname, struct cli_ac_data *mdata,
uint32_t offset,
const struct cli_target_info *tinfo,
cli_file_t ftype,
struct cli_matched_type **ftoffset,
unsigned int acmode,
unsigned int pcremode,
struct cli_ac_result **acres,
fmap_t *map,
struct cli_bm_off *offdata,
struct cli_pcre_off *poffdata,
cli_ctx *ctx
)ここでは、cli_bm_scanbuff 関数にて Boyer-Moore 法(をベースにしたアルゴリズム)によるスキャンを実施した後に、cli_ac_scanbuff 関数で Aho-Corasick アルゴリズムによるパターンマッチングを行います。
cli_ac_scanbuff 関数については前回まとめたので、今回は cli_bm_scanbuff 関数による Boyer-Moore 法を使用したスキャンについてまとめます。
Boyer–Moore(BM) 法とは
BM 法は、特定のテキストの中に指定のキーワード(シグネチャ)が含まれているか否かを高速に検索可能なアルゴリズムです。
BM 法の基本的なアイデアとしては、キーワードのパターンに対して前処理を行い、「キーワードの末尾から先頭に向かって文字を比較すること」と「可能な限り無駄なチェックを省いて検索対象の文字列とキーワードの一致を検査すること」により高速なキーワード検索を実現するものです。
標準的な BM 法は、後述する Bad Character Rule(不一致文字規則) と Good Suffix Rule(一致接尾辞規則) という 2 つのルールを適用したものを指すようです。
この標準的な BM 法は最悪計算量が O(N*M) (テキストの長さ N × キーワードの長さ M) となりますが、さらにガリル規則というルールを追加することで、最悪計算量を線形時間に圧縮できるようになるようです。
また、BM 法の派生として、Bad Character Rule(不一致文字規則) のみを利用し、さらに BM 法を簡略化した Boyer–Moore–Horspool(BMH) 法というアルゴリズムも存在しています。
ClamAV のような AntiVirus ソフトウェアのシグネチャパターンマッチング処理では、いくつかの理由から BM 法の中でもこの Boyer–Moore–Horspool(BMH) 法が利用される場合があるようなので、今回はこの BMH 法をメインに扱います。
Bad Character Rule(不一致文字規則)
BM 法における Bad Character Rule は、テキスト内でキーワードと一致しなかった文字が発見された場合、その文字がキーワード内のどこにあるかを基準に不要なチェックをスキップするためのルールです。
Bad Character Rule については、以下の記事で紹介されている図がわかりやすかったです。
参考:文字列検索アルゴリズム③ ー Boyer-Moore法 #競技プログラミング - Qiita
BM 法のチェックにおいては、検索対象の文字列 S とキーワード T を比較する際に、キーワード T の先頭と文字列 S の検索位置をそろえた後、キーワードの末尾の位置のワードから順に、検索対象の文字列とキーワードが一致するかを比較します。
ここで、検索対象の文字とキーワードの文字に不一致が発生した場合に、「可能な限り次の検索位置を大きくずらす」ことで効率的な文字列検索を行うのが Bad Character Rule です。
Bad Character Rule では、検索対象のキーワードの前処理によりずらし表(不一致が発生した場合に何文字検索位置をずらすことができるか)を作成しておき、末尾で不一致が発生した文字に応じて最大限検索位置をスキップします。
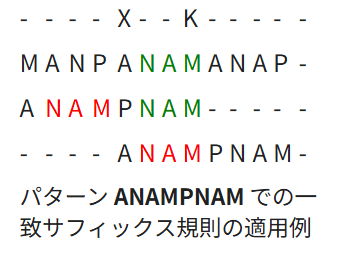
例えば、Wikipedia の説明の例だと、キーワード NNAAMAN とテキストを末尾から比較していき、不一致が発生した「N」の箇所でルールの評価を行います。
この文字「N」は、その位置の左側に同じ文字が含まれていればその位置まで、キーワード内に含まれていない文字の場合は、キーワードにマッチする可能性がなくなるためその次の文字の位置まで検索位置をスキップします。
参考:ボイヤー-ムーア文字列検索アルゴリズム - Wikipedia
Bad Character Rule の実装
Bad Character Rule による文字列の検索の理解を深めるため、各検索ステップを可視化する Python スクリプトを作成しました。
以下のスクリプトの BMSearcher クラスでは検索対象のキーワードを前処理して Bad Character Table を作成します。
class BMSearcher:
def __init__(self, pattern: str):
self.pattern = pattern
self.m = len(pattern)
# Bad Character Table の作成
self._bad_char_table: Dict[str, int] = self._build_bad_char_table()
def _build_bad_char_table(self) -> Dict[str, int]:
# Skip table: Dict[str, int]
# 検索対象のキーワード内の文字と、その文字がキーワード内で最後に出現する位置のインデックス
table = {}
for i, char in enumerate(self.pattern):
table[char] = i
return tableBad Character Table は、検索対象のキーワードに含まれる文字をキーとして、その文字がキーワード内で最後に(最も右側に)出現する位置のインデックスを示す辞書として定義します。
これにより、検索時に文字の不一致が発生した場合、次の検索位置をどこまでスキップできるかを決定します。
上記の検索処理を実装したコードは以下の通りです。
@dataclass(frozen=True)
class SearchStep:
shift: int # シフト位置
mismatch_index: Optional[int] # 不一致が発生したインデックス(末尾からの相対位置)
bad_char: Optional[str] # 不一致となった文字
shift_amount: int # 次のステップのためのシフト量
description: str # 説明
class BMSearcher:
def __init__(self, pattern: str):
self.pattern = pattern
self.m = len(pattern)
# Bad Character Table の作成
self._bad_char_table: Dict[str, int] = self._build_bad_char_table()
def _build_bad_char_table(self) -> Dict[str, int]:
# Skip table: Dict[str, int]
# 検索対象のキーワード内の文字と、その文字がキーワード内で最後に出現する位置のインデックス
table = {}
for i, char in enumerate(self.pattern):
table[char] = i
return table
# 検索処理の可視化のため、検索中の状態を返す Generator 関数
def search_generator(self, text: str) -> Iterator[SearchStep]:
n = len(text)
shift = 0
while shift <= n - self.m:
j = self.m - 1
# 末尾から順にキーワードとテキストの一致を比較する
while j >= 0 and self.pattern[j] == text[shift + j]:
j -= 1
# 文字列が完全に一致した場合
if j < 0:
yield SearchStep(
shift=shift,
mismatch_index=None,
bad_char=None,
shift_amount=1,
description="Complete match found!"
)
shift += 1
# 検索中に不一致が発生した場合
else:
text_char = text[shift + j]
# Bad Character Rule の計算式: shift_amount = max(1, mismatch_index - last_occurrence_index)
last_occurrence = self._bad_char_table.get(text_char, -1)
# スキップのためのシフト量(ループ回避のため最低 1 はシフトさせる)
shift_amount = max(1, j - last_occurrence)
reason = (
f"Bad char '{text_char}' found at pattern index {last_occurrence}."
if last_occurrence != -1 and last_occurrence < j
else f"Bad char '{text_char}' logic (not in pattern or to right)."
)
yield SearchStep(
shift=shift,
mismatch_index=j,
bad_char=text_char,
shift_amount=shift_amount,
description=reason
)
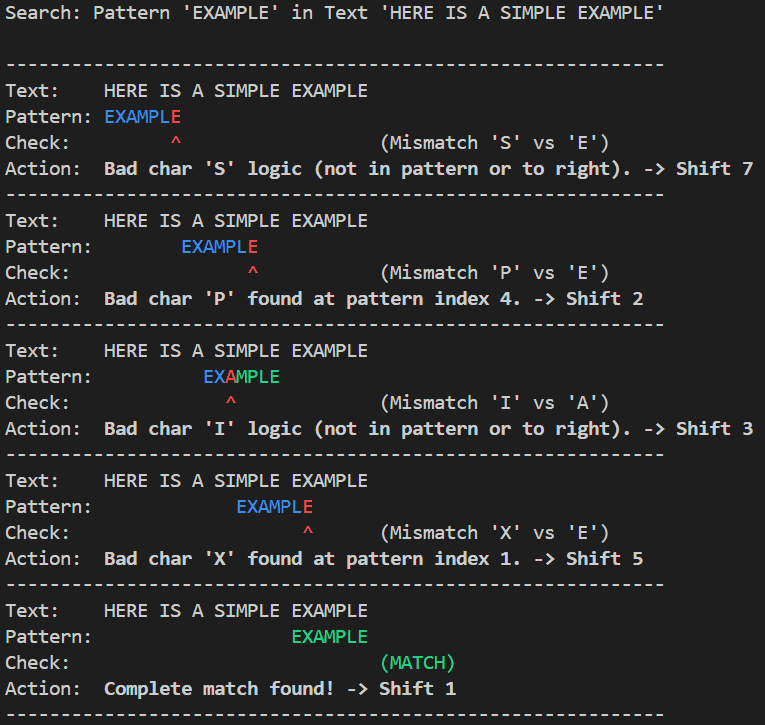
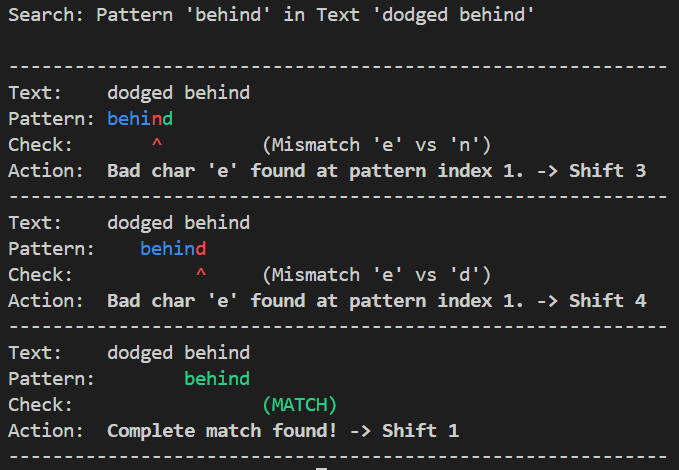
shift += shift_amount上記をベースにしたスクリプトを実行すると、以下のように Bad Character Rule による末尾からの文字検索と、不一致が発生した場合の検索位置のシフト動作をみることができます。
Good Suffix Rule(一致接尾辞規則)
Good Suffix Rule は Bad Character Rule 単体より効率的な検索を行うために追加されるルールです。
概要レベルですが、Good Suffix Rule では末尾から評価した際に一致した部分があれば、それを Good Suffix として検索位置の決定に利用することでより効率的なスキャンを実現しようとするアイデアです。
参考:ボイヤー-ムーア文字列検索アルゴリズム - Wikipedia
一般的には、この Bad Character Rule と Good Suffix Rule を使用するアルゴリズムが標準的な BM 法とされるようです。
さらに、ガリル規則とよばれるルールを追加する場合もあります。
しかし、Good Suffix Heuristic を加えた標準の BM 法や、ガリル規則を加えて線形時間での検索を保証した BM 法は、理論上はより効率的に動作しますが、実装の複雑やや前処理のためのコストがかかるなどの点から、実務上での利用には適さないケースがあるようです。
そのため、実装のシンプルさや平均的な速さが求められる一般的なテキストエディタの検索機能や、今回のターゲットである AntiVirus のパターンマッチング処理などにおいては、Bad Character Rule のみを用いた BM 法や、それを簡略化した Boyer–Moore–Horspool(BMH) 法やそれをベースにしたアルゴリズムが用いられることが多いようです。
※ なお、ClamAV などの AntiVirus の場合は単純な BMH 法ではなく、複数のパターンを多重的に検索するために拡張された Wu-Manber 法に近い処理が使用されているようです。
参考:AFASTALGORITHMFORMULTI-PATTERNSEARCHING
参考:Practical Fast Searching in Strings
Boyer–Moore–Horspool(BMH) 法
Boyer–Moore–Horspool(BMH) 法は、前述の通り BM 法から Good Suffix Rule を省いたものをベースにし、簡略化したアルゴリズムです。
ガリル規則を加えた BM 法では、文字列検索のマッチング処理における最悪計算量は O(N) であることが保証されるため、O(NM) である BMH 法より理論上は高速なアルゴリズムとされています。
ただし、ClamAV では BMH 法をベースにしたアルゴリズムがパターンマッチング処理に利用されています。
実際には、 Good Suffix Rule やガリル規則を含めた BM 法は、理論上の最悪計算量は BMH 法より高速であるものの、前処理にかかるコストなども含めて考えると、いくつかのユースケースでは BMH 法の方が平均的なパフォーマンスが良くなる場合があるため、アプリケーションによって BM 法ではなく BMH 法が採用される場合も少なくないようです。
参考:Boyer-Moore vs Boyer-Moore-Horspool Search Algorithms | Search Algorithms | StudyPlan.dev
参考:Boyer-Moore algorithm - コードの恵み
BMH 法と BM 法の Bad Character Rule の違いについては、以下のページの説明が最もわかりやすかったです。
参考:Algorithms with Python / 文字列の探索
BMH 法は、一言でいうと「パターンの不一致が発生した場合には常に末尾の文字に着目し、できるだけ大きく検索をスキップする」ような手法です。
前述した通り、Bad Character Rule では不一致が発生した場合には検索対象のキーワードに含まれる文字をキーとし、その文字がキーワード内で最後に(最も右側に)出現する位置のインデックスを示す辞書として定義してスキップを行います。
つまり、以下の例のように 1 回目の検索で末尾から 2 番目の文字 e で不一致が発生した場合、Bad Character Rule では不一致が発生した e の位置ををそろえて次のマッチング処理を行います。
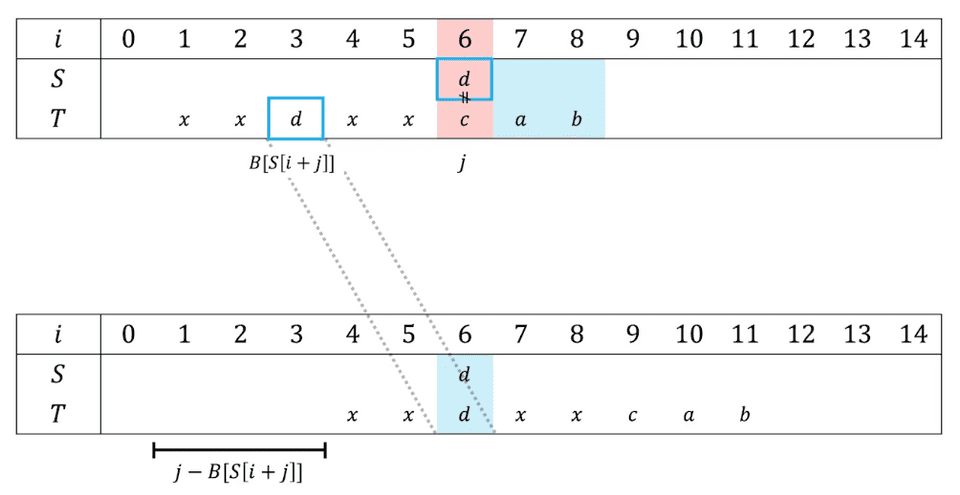
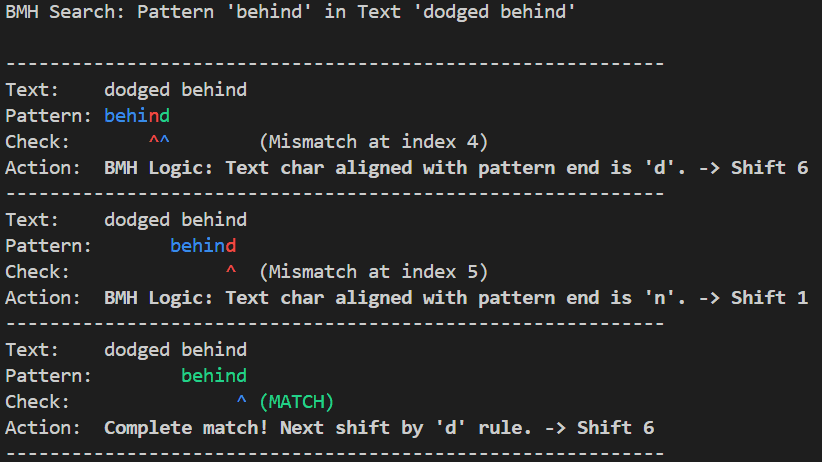
一方で、BMH 法を使用する場合は不一致がどこで発生した場合でも末尾の文字に着目し、その末尾の文字がキーワード内の最も右側に現れる位置に検索位置をスライドさせます。
(以下の例のように、末尾の文字 d がキーワードに含まれない場合には、次の文字にキーワードの先頭をそろえてチェックを行います。)
これにより、BMH 法を使用する場合はチェックがどの位置で失敗したかを考慮する必要がなく末尾の文字のみに着目できるので Bad Character Rule と比較して実装がシンプルになり、また Bad Character Rule よりも大きく検索位置をシフトできるようになります。
BMH が使用するテーブル作成処理を Python で実装した結果は以下のようになりました。
class BMHSearcher:
def __init__(self, pattern: str):
self.pattern = pattern
self.m = len(pattern)
self._shift_table: Dict[str, int] = self._build_shift_table()
def _build_shift_table(self) -> Dict[str, int]:
table = {}
# パターンの最後の文字以外 (0 から m-2 まで) を登録
for i in range(self.m - 1):
char = self.pattern[i]
table[char] = self.m - 1 - i
return tableBad Character Rule の実装とほぼ同じですが、テーブルに含まれる情報が、キーワード内の文字がキーワード内で最後に出現する位置のインデックスではなく、末尾の文字からの距離に変わっている点に違いがあります。
Wu-Manber (WM) 法
Wu-Manber (WM) 法は、BMH 法のアイデアをベースに複数のパターンを同時に検索する方法として考案された検索アルゴリズムです。
末尾文字の不一致を利用してできるだけ大きくスキップを行うことで検索の効率化を目指す BMH 法の考え方は、末尾の文字がキーワード内に含まれない確率が高いほどより大きく検索位置をシフトして高効率化を実現できるものです。
しかし、もし検索対象のパターンの数が増えた場合にはパターンの集合内のいずれかの文字が末尾の文字に一致する確率が高まり、最終的に大きなシフト幅を得られない状態に収束してしまいます。
このようなマルチパターン検索の問題を解決するため、WM 法では特定の文字ではなく通常は 2 or 3 文字のブロック単位で評価を行い、検索位置をスキップします。
WM 法ではまず、前処理段階でパターンの集合の中で最小の長さを m、通常は 2 か 3 が使用されるブロックサイズを B とし、各パターンの先頭 m 文字を用いて SHIFT、HASH、PREFIX の 3 つのテーブルを作成します。
SHIFT テーブルは BM のシフトテーブルを拡張したもので、テキストスキャン時にテキスト内の文字をどれだけスキップできるかを決定するために使用されます。
また、HASH テーブルにはサフィックス(パターンの先頭から m 文字抜き出した文字列の末尾の B 文字)が同じパターンのリストへのポインタが、PREFIX テーブルには各パターンのプレフィックス(先頭から B 文字)のハッシュ値が含まれ、パターンマッチング処理に使用されます。
この前処理を Python で以下のように実装しました。
class WuManber:
def __init__(self, patterns: List[str], block_size: int = 2) -> None:
if not patterns:
raise ValueError("Invalid patterns.")
self.patterns = patterns
self.block_size = block_size
self.min_len = min(len(p) for p in patterns)
if self.min_len < self.block_size:
raise ValueError(f"Block size {self.block_size} is larger than the minimum pattern length {self.min_len}.")
# SHIFT テーブル
self.shift_table: Dict[str, int] = {}
# HASH テーブル
self.hash_table: Dict[str, List[int]] = defaultdict(list)
# PREFIX テーブル / Python の組込み関数 hash() は整数を返すのでそのまま利用
self.prefix_table: List[int] = []
self._build_tables()
def _get_hash(self, text_block: str) -> int:
return hash(text_block)
def _build_tables(self) -> None:
for idx, pattern in enumerate(self.patterns):
prefix_part = pattern[:self.block_size]
self.prefix_table.append(self._get_hash(prefix_part))
limit_pattern = pattern[:self.min_len]
# shift_table: {'ap': 3, 'pp': 2, 'pl': 1, 'le': 0, 'am': 3}
for i in range(self.min_len - self.block_size + 1):
block = limit_pattern[i : i + self.block_size]
shift = self.min_len - 1 - (i + self.block_size - 1)
if block not in self.shift_table:
self.shift_table[block] = shift
else:
self.shift_table[block] = min(self.shift_table[block], shift)
if shift == 0:
self.hash_table[block].append(idx)まず、以下の初期化処理では、検索対象のキーワードのリストである patterns と、既定のブロックサイズ 2 を用いて各種テーブルの作成を行います。
def __init__(self, patterns: List[str], block_size: int = 2) -> None:
if not patterns:
raise ValueError("Invalid patterns.")
self.patterns = patterns
self.block_size = block_size
self.min_len = min(len(p) for p in patterns)
if self.min_len < self.block_size:
raise ValueError(f"Block size {self.block_size} is larger than the minimum pattern length {self.min_len}.")
# SHIFT テーブル
self.shift_table: Dict[str, int] = {}
# HASH テーブル
self.hash_table: Dict[str, List[int]] = defaultdict(list)
# PREFIX テーブル / Python の組込み関数 hash() は整数を返すのでそのまま利用
self.prefix_table: List[int] = []
self._build_tables()この時、全パターンの中で最も短いパターンの長さを minlen として保持します。(この minlen がブロックサイズより小さい場合には標準の WU 法による検索を使用できません。)
実際に各種テーブルの作成を行う _build_tables メソッドは以下のように実装しています。
def _build_tables(self) -> None:
for idx, pattern in enumerate(self.patterns):
prefix_part = pattern[:self.block_size]
self.prefix_table.append(self._get_hash(prefix_part))
limit_pattern = pattern[:self.min_len]
for i in range(self.min_len - self.block_size + 1):
block = limit_pattern[i : i + self.block_size]
shift = self.min_len - 1 - (i + self.block_size - 1)
if block not in self.shift_table:
self.shift_table[block] = shift
else:
self.shift_table[block] = min(self.shift_table[block], shift)
if shift == 0:
self.hash_table[block].append(idx)この中では、パターンのリストに対してループ処理を行い、まずパターンの先頭 B 文字分(pattern[:self.block_size]) を Python の組込み関数 hash() でハッシュ化した整数値を PREFIX テーブルとしてリストに後方追加しています。
※ これにより、パターンのインデックスを用いて PREFIX テーブルから先頭ブロックのハッシュを取得できます。
続いて、パターンの先頭 m 文字を limit_pattern = pattern[:self.min_len] として保存した後に m - B + 1 分のループ処理を行い、その中で SHIFT テーブルの作成を実施します。
ここでは、各パターンの先頭 m 文字分の中から長さ B のブロックを順に取り出していき、ブロックごとに安全にシフトできるシフト量を SHIFT テーブルに追加します。
また、ブロックが m 文字のパターンの末尾のブロックである(shift == 0)場合には、そのブロックを キーとするリストにパターンインデックスを追加し、HASH テーブルを作成します。
block = limit_pattern[i : i + self.block_size]
shift = self.min_len - 1 - (i + self.block_size - 1)
if block not in self.shift_table:
self.shift_table[block] = shift
else:
self.shift_table[block] = min(self.shift_table[block], shift)
if shift == 0:
self.hash_table[block].append(idx)これで、WU 法による検索を行うために必要なテーブルの作成が完了しました。
続いて、このテーブルを使用したテキスト検索処理(search 関数)を見ていきます。
def search(self, text: str) -> Iterator[Tuple[int, str]]:
n = len(text)
m = self.min_len
B = self.block_size
if n < m:
return
idx = m - 1
default_shift = m - B + 1
while idx < n:
# 末尾ブロックを取得してシフト量を決定
suffix_block = text[idx - B + 1 : idx + 1]
shift = self.shift_table.get(suffix_block, default_shift)
# シフト量が0の場合、候補パターンと比較(それ以外はシフト)
if shift == 0:
candidate_indices = self.hash_table.get(suffix_block, [])
text_start_pos = idx - m + 1
text_prefix_block = text[text_start_pos : text_start_pos + B]
text_prefix_hash = self._get_hash(text_prefix_block)
for p_idx in candidate_indices:
if self.prefix_table[p_idx] != text_prefix_hash:
continue
pattern = self.patterns[p_idx]
p_len = len(pattern)
if text_start_pos + p_len <= n:
if text[text_start_pos : text_start_pos + p_len] == pattern:
yield (text_start_pos, pattern)
idx += 1
else:
idx += shiftsearch 関数が呼び出された際には、まずテキストの m 文字分を取り出し、その末尾 B 文字を suffix_block として抜き出して SHIFT テーブルと比較します。
末尾 B 文字が SHIFT テーブル内に存在しない場合は m - B + 1、SHIFT テーブル内に存在する場合はテーブルに保存されているシフト量で検索位置を移動します。
また、シフト量が 0 の場合には、パターンが現在の検索位置に含まれている可能性があるため、そのブロックが末尾に含まれるパターンのインデックスが含まれるリストを HASH テーブルから candidate_indices として取り出します。
続けて、そのブロックが末尾に含まれるパターンの先頭のブロックのハッシュを PREFIX テーブルから取り出したあと検索位置のテキストの先頭ブロックのハッシュと比較し、一致する場合にはテキストの全文検索を行いパターンとのマッチングを行います。
ここで、PREFIX テーブルによる先頭部分のマッチングを行う理由は、英文から単語を検索するような場合、tion や ee など多くの単語に共通して含まれる末尾のブロックが頻繁にマッチする可能性があるためのようです。
そのため、末尾のブロックだけでなく、先頭のブロックについてもチェックを行い、マッチしたもののみに対してパターンの全文検索を行うことで効率化が可能になります。
参考:AFASTALGORITHMFORMULTI-PATTERNSEARCHING
参考:Variations of Wu-Manber String Matching Algorithm
参考:wumanber/wumanber.hpp at master · bubiche/wu_manber
ClamAV の実装を読む
ここまでに BM 法や BMH 法、またその考え方をベースにマルチパターンマッチングに対応した WU 法についてまとめてきました。
ここからは、ClamAV の cli_bm_scanbuff 関数の実際の実装を読み、AntiVirus におけるパターンマッチング処理の実装を確認していきます。
関数の呼び出し
cli_bm_scanbuff という関数名の bm は BM 法を意味するもので、「Extended Boyer-Moore」として実装されており、実際の処理は WU 法に近い動作になっています。
cli_bm_scanbuff 関数は、以下のパラメーターと共に呼び出され、clamscan によるファイルスキャンの場合にはスキャン対象のファイル内のデータが buffer として渡されます。
cl_error_t cli_bm_scanbuff(
const unsigned char *buffer,
uint32_t length,
const char **virname,
const struct cli_bm_patt **patt,
const struct cli_matcher *root,
uint32_t offset,
const struct cli_target_info *info,
struct cli_bm_off *offdata,
cli_ctx *ctx
);前処理によるテーブルの作成
ClamAV の「Extended Boyer-Moore」の動作は実質的に WU 法に近いものですので、SHIFT テーブルや HASH テーブルなどの作成のための前処理が必要になります。
これらのテーブルの作成は cli_bm_scanbuff では行われず、root として渡される cli_matcher のオブジェクトに含まれているようです。
struct cli_matcher {
unsigned int type;
/* Extended Boyer-Moore */
uint8_t *bm_shift;
struct cli_bm_patt **bm_suffix, **bm_pattab;
uint32_t *soff, soff_len; /* for PE section sigs */
uint32_t bm_offmode, bm_patterns, bm_reloff_num, bm_absoff_num;
/* HASH */
struct cli_hash_patt hm;
struct cli_hash_wild hwild;
/* Extended Aho-Corasick */
uint32_t ac_partsigs, ac_nodes, ac_lists, ac_patterns, ac_lsigs;
struct cli_ac_lsig **ac_lsigtable;
struct cli_ac_node *ac_root, **ac_nodetable;
struct cli_ac_list **ac_listtable;
struct cli_ac_patt **ac_pattable;
struct cli_ac_patt **ac_reloff;
uint32_t ac_reloff_num, ac_absoff_num;
uint8_t ac_mindepth, ac_maxdepth;
struct filter *filter;
uint16_t maxpatlen;
uint8_t ac_only;
{省略}
};WU 法で言うところの SHIFT テーブルは bm_shift に該当しており、cli_bm_addpatt 関数でマッチング対象のパターンごとに値が設定されます。
スキャン処理
cli_bm_scanbuff 関数におけるスキャン処理は以下の通り、前述した WU 法のスキャンと同じように実装されています。
スキャン対象のデータである buffer から 3 文字ずつ抜き出し、それを独自のマクロでハッシュ化した整数値をインデックスとして SHIFT テーブルのチェックを行います。
#define BM_MIN_LENGTH 3
#define BM_BLOCK_SIZE 3
#define HASH(a, b, c) (211 * a + 37 * b + c)
{省略}
i = BM_MIN_LENGTH - BM_BLOCK_SIZE;
for (; i < length - BM_BLOCK_SIZE + 1;) {
idx = HASH(buffer[i], buffer[i + 1], buffer[i + 2]);
shift = root->bm_shift[idx];
if (shift == 0) {
prefix = buffer[i - BM_MIN_LENGTH + BM_BLOCK_SIZE];
p = root->bm_suffix[idx];
if (p && p->cnt == 1 && p->pattern0 != prefix) {
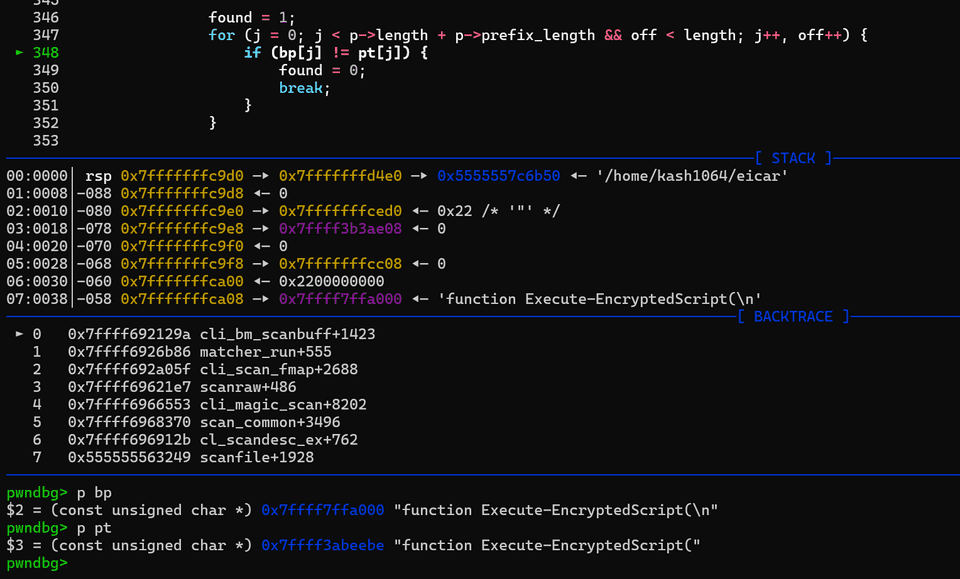
{省略}さらに、SHIFT テーブルのシフト量が 0 の場合には、PREFIX テーブルと HASH テーブルのチェックを行った上で、バッファとパターンの照合を行い、一致した場合には最終的に CL_VIRUS を返して検出を行います。
まとめ
今回は前回の Aho–Corasick アルゴリズムに続き、AntiVirus を支える情報検索アルゴリズムとして、BM 法やそこから発展した WU 法についてまとめました。