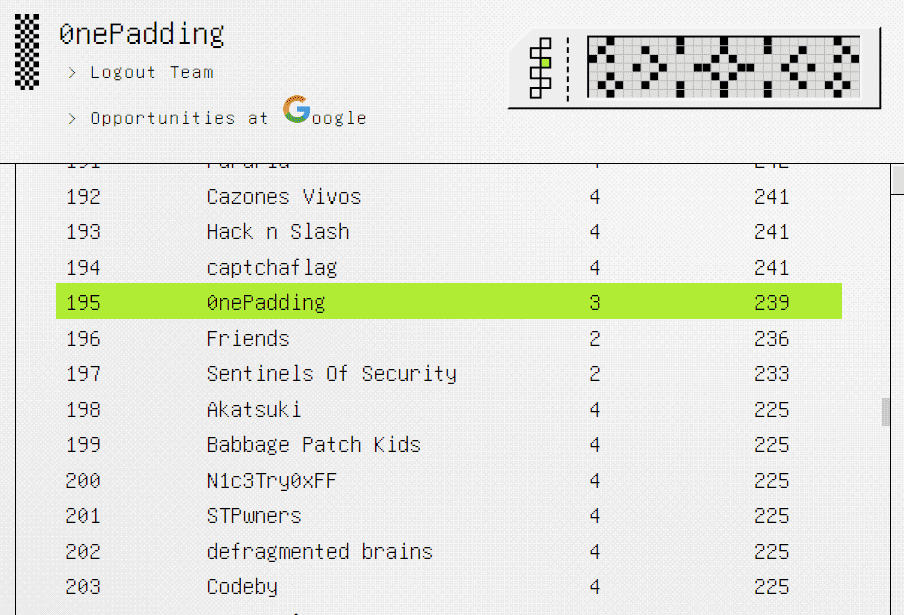
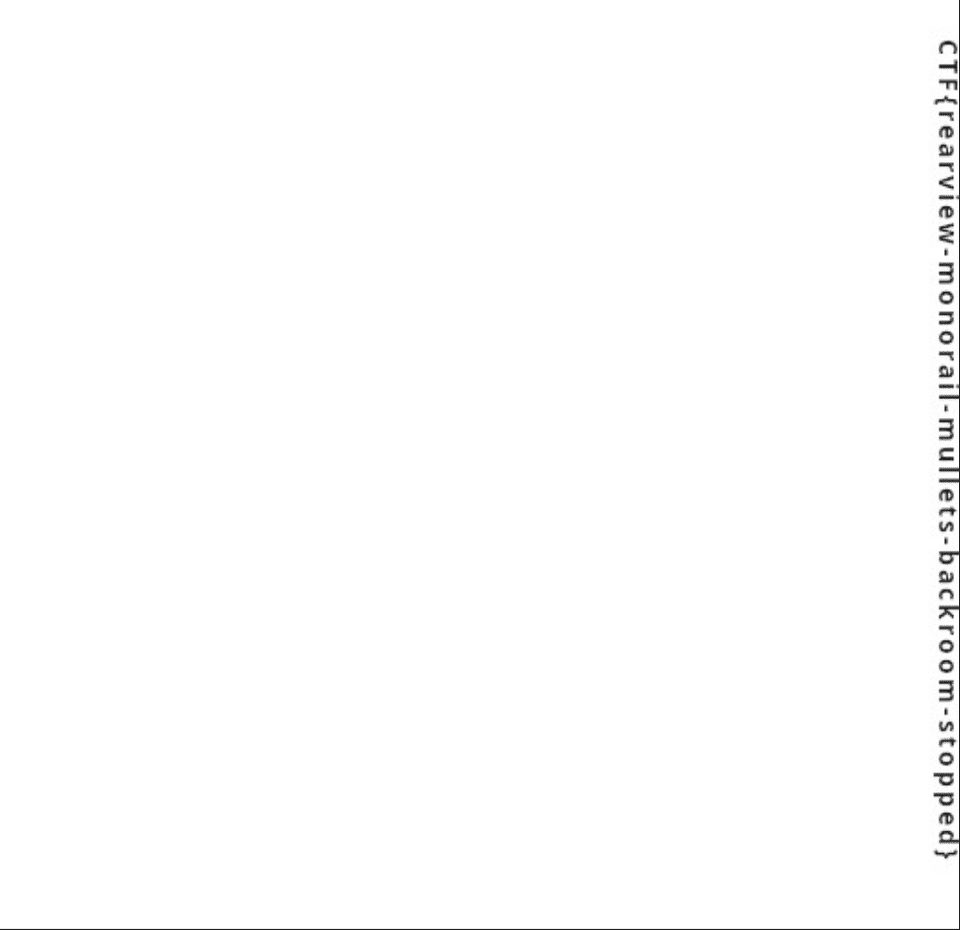All Articles

Google CTF 2023 Writeup

6/24 から開催されていた Google CTF 2023 に 0nePadding で参加して 195 位でした。

今回は Rev、Crypto、Misc を 1 問ずつ解きました。

去年と一昨年は参加したものの 1 問も解けずに撤退という感じでスコアボードにすら乗れずに終わっていたので、ちょっとした成長を実感できる機会でした。

image-20230626081855374

また、Crypto の問題は 1 人では解けず、チームメンバーと相談しながら進めたおかげで解けたものだったので、0nePadding のチームとしても去年より活発に動いていることを実感しました。

解けなかった問題は後日復習するとして、とりあえず解けた問題のみまとめておきます。

もくじ

ZERMATT(Rev)

Roblox made lua packing popular, since we’d like to keep hanging out with the cool kids, he’s our take on it.

問題バイナリとして非常に長い難読化された lua スクリプトファイルが与えられます。

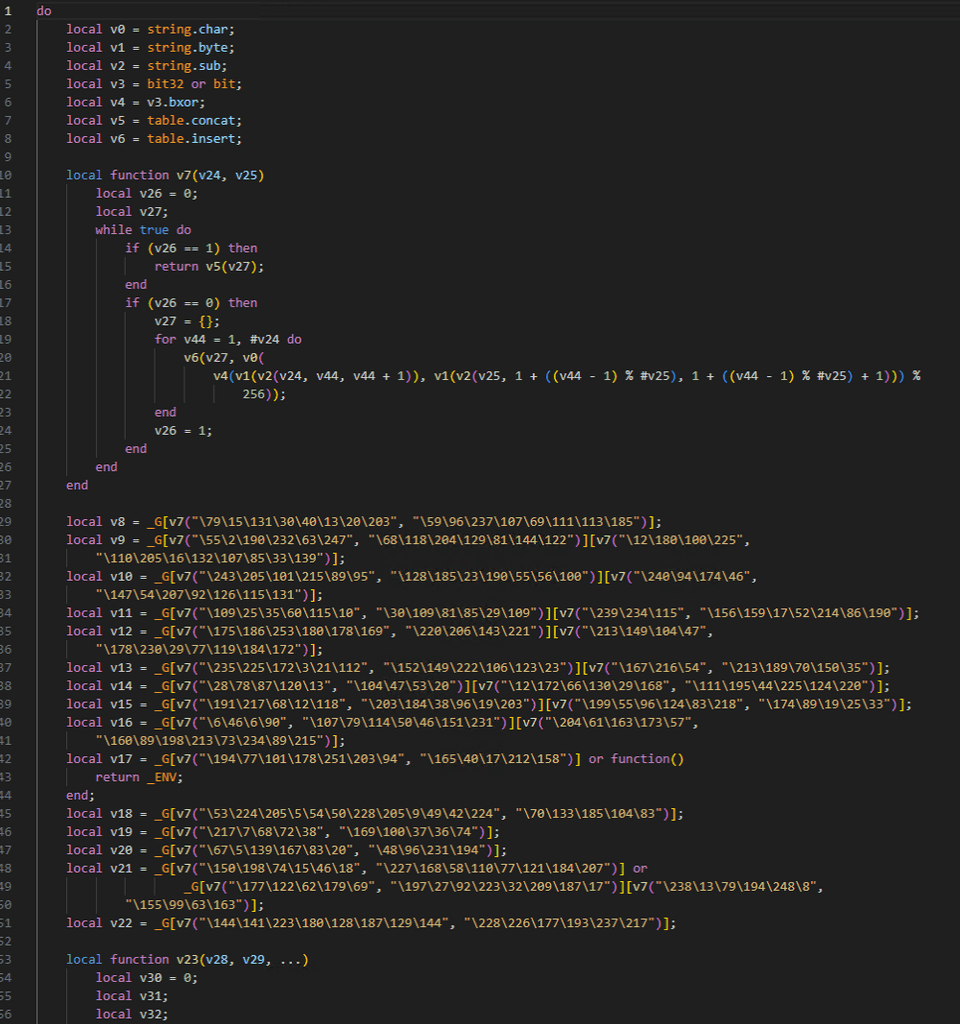
難読化されたスクリプトを整形して表示してみると 3000 行くらいのボリュームになりましたが、以下のように冒頭部分でごちゃごちゃした処理をしていることがわかります。

image-20230626232514302

よく見ると、v7 という関数に 2 つのバイト文字を与えた戻り値を lua のグローバル環境変数 _G のキーとして与えています。

ここで、以下のようなスクリプトを使ってそれぞれの処理結果を見てみました。

local v0 = string.char;
local v1 = string.byte;
local v2 = string.sub;
local v3 = bit32 or bit;
local v4 = v3.bxor;
local v5 = table.concat;
local v6 = table.insert;
local function v7(v24, v25)
    local v26 = 0;
    local v27;
    while true do
        if (v26 == 1) then
            return v5(v27);
        end
        if (v26 == 0) then
            v27 = {};
            for v44 = 1, #v24 do
                v6(v27, v0(
                    v4(v1(v2(v24, v44, v44 + 1)), v1(v2(v25, 1 + ((v44 - 1) % #v25), 1 + ((v44 - 1) % #v25) + 1))) % 256));
            end
            v26 = 1;
        end
    end
end

print(v7("\79\15\131\30\40\13\20\203", "\59\96\237\107\69\111\113\185"))
print(v7("\55\2\190\232\63\247", "\68\118\204\129\81\144\122"))
print(v7("\12\180\100\225", "\110\205\16\132\107\85\33\139"))
print(v7("\243\205\101\215\89\95", "\128\185\23\190\55\56\100"))
print(v7("\240\94\174\46","\147\54\207\92\126\115\131"))
print(v7("\109\25\35\60\115\10", "\30\109\81\85\29\109"))
print(v7("\239\234\115", "\156\159\17\52\214\86\190"))
print(v7("\175\186\253\180\178\169", "\220\206\143\221"))
print(v7("\213\149\104\47", "\178\230\29\77\119\184\172"))
print(v7("\235\225\172\3\21\112", "\152\149\222\106\123\23"))
print(v7("\167\216\54", "\213\189\70\150\35"))
print(v7("\28\78\87\120\13", "\104\47\53\20"))
print(v7("\12\172\66\130\29\168", "\111\195\44\225\124\220"))
print(v7("\191\217\68\12\118", "\203\184\38\96\19\203"))
print(v7("\199\55\96\124\83\218", "\174\89\19\25\33"))
print(v7("\6\46\6\90", "\107\79\114\50\46\151\231"))
print(v7("\204\61\163\173\57", "\160\89\198\213\73\234\89\215"))
print(v7("\194\77\101\178\251\203\94", "\165\40\17\212\158"))
print(v7("\53\224\205\5\54\50\228\205\9\49\42\224", "\70\133\185\104\83"))
print(v7("\217\7\68\72\38", "\169\100\37\36\74"))
print(v7("\67\5\139\167\83\20", "\48\96\231\194"))
print(v7("\150\198\74\15\46\18", "\227\168\58\110\77\121\184\207"))
print(v7("\177\122\62\179\69", "\197\27\92\223\32\209\187\17"))
print(v7("\238\13\79\194\248\8", "\155\99\63\163"))
print(v7("\144\141\223\180\128\187\129\144", "\228\226\177\193\237\217"))

これを実行すると以下のような文字列がデコードされます。

これを引数として与えることで、関数を変数に格納しようとしていることがわかります。

image-20230626234434239

この結果を元に難読化されたスクリプトを復元してみると以下のようになりました。

local v8 = _G["tonumber"];
local v9 = _G["string"]["byte"];
local v10 = _G["string"]["char"];
local v11 = _G["string"]["sub"];
local v12 = _G["string"]["gsub"];
local v13 = _G["string"]["rep"];
local v14 = _G["table"]["concat"];
local v15 = _G["table"]["insert"];
local v16 = _G["math"]["ldexp"];
local v17 = _G["getfenv"] or function() return _ENV; end;
local v18 = _G["setmetatable"];
local v19 = _G["pcall"];
local v20 = _G["select"];
local v21 = _G["unpack"] or _G["table"]["unpack"];
local v22 = _G["tonumber"];

ここでは、lua のグローバルテーブルを使用して各関数のアドレスを変数に保存しているようです。

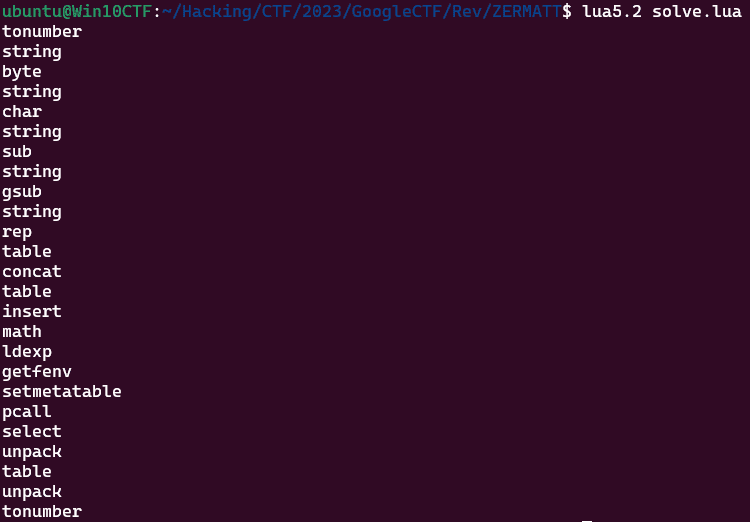
僕の環境の lua5.2 を使用した場合のグローバルテーブルには、以下のような定義が行われていました。

for n in pairs(_G) do print(n) end
>
pairs
loadstring
package
tostring
load
rawlen
_G
setmetatable
assert
require
error
os
unpack
getmetatable
string
dofile
tonumber
_VERSION
rawequal
collectgarbage
bit32
coroutine
debug
table
io
pcall
type
math
xpcall
next
arg
module
rawget
loadfile
print
ipairs
select
rawset

参考：Programming in Lua : 14

この結果を元に関数が代入された変数を置き換えてあげると、多少コードが読みやすくなります。

そして、さらに問題バイナリを読み解いていくと、かなりの量の不要な処理でコード量のかさ増しが行われていることがわかります。

例えば、以下のようなコードです。

if (v89 == 0) then
    local v130 = 0;
    while true do
        if (v130 == 1) then
            v89 = 1; break;
        end
        if (0 == v130) then
            v90 = nil; 
            if not v87 then
                local v166 = 0; local v167;
                while true do if (v166 == 0) then
                        v167 = 0; 
                        while true do if (v167 == 0) then
                                v87 = v37(); 
                                if (v87 == 0) then return ""; end
                                break;
                            end 
                        end
                        break;
                    end 
                end
            end
            v130 = 1;
        end
    end
end

よく見てみると、最終的にv87 = v37();の定義を行ったのみでループを抜け出しています。

このような構造がスクリプト内にいくつも存在しているため、これらの処理を削除していくことで難読化を解除していくことが可能です。

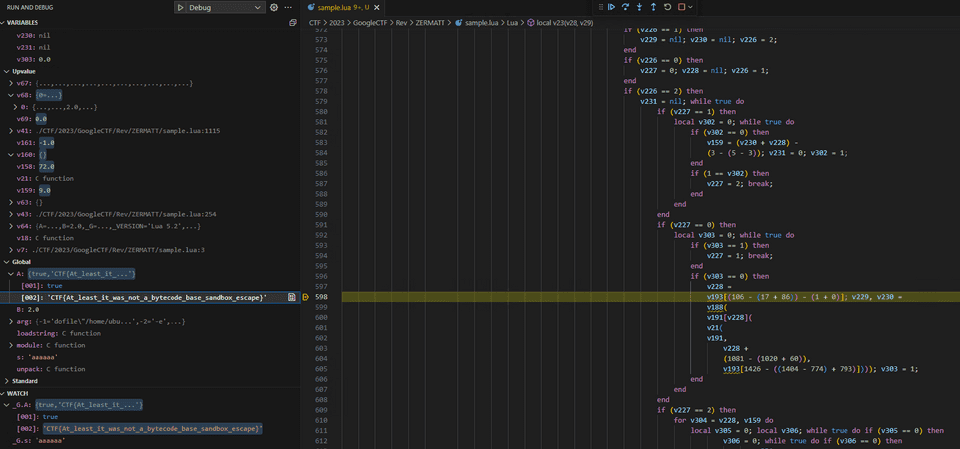
不要な処理をある程度削ったところでデバッガを駆使しながらプログラムの動作を追っていくと、以下のように正しい Flag を一文字ずつ取得しているコードが見つかります。

image-20230625163128387

これで Flag を取得できました。

正解時のアニメーションがおしゃれでした。

image-20230625163221330

LEAST COMMON GENOMINATOR?(Crypto)

Someone used this program to send me an encrypted message but I can’t read it! It uses something called an LCG, do you know what it is? I dumped the first six consecutive values generated from it but what do I do with it?!

珍しく Crypto を 1 問解いたので書いておきます。

問題バイナリとして与えられた以下のスクリプトを読みました。

どうやら LCG(Linear Congruential Generator) によって生成された素数を使用して生成した鍵で Flag を暗号化しているようだということがわかります。

from secret import config
from Crypto.PublicKey import RSA
from Crypto.Util.number import bytes_to_long, isPrime

class LCG:
    lcg_m = config.m
    lcg_c = config.c
    lcg_n = config.n

    def __init__(self, lcg_s):
        self.state = lcg_s

    def next(self):
        self.state = (self.state * self.lcg_m + self.lcg_c) % self.lcg_n
        return self.state

if __name__ == '__main__':

    assert 4096 % config.it == 0
    assert config.it == 8
    assert 4096 % config.bits == 0
    assert config.bits == 512

    # Find prime value of specified bits a specified amount of times
    seed = 211286818345627549183608678726370412218029639873054513839005340650674982169404937862395980568550063504804783328450267566224937880641772833325018028629959635
    lcg = LCG(seed)
    primes_arr = []
    
    dump = True
    items = 0
    dump_file = open("dump.txt", "w")

    primes_n = 1
    while True:
        for i in range(config.it):
            while True:
                prime_candidate = lcg.next()
                if dump:
                    dump_file.write(str(prime_candidate) + '\n')
                    items += 1
                    if items == 6:
                        dump = False
                        dump_file.close()
                if not isPrime(prime_candidate):
                    continue
                elif prime_candidate.bit_length() != config.bits:
                    continue
                else:
                    primes_n *= prime_candidate
                    primes_arr.append(prime_candidate)
                    break
        
        # Check bit length
        if primes_n.bit_length() > 4096:
            print("bit length", primes_n.bit_length())
            primes_arr.clear()
            primes_n = 1
            continue
        else:
            break

    # Create public key 'n'
    n = 1
    for j in primes_arr:
        n *= j
    print("[+] Public Key: ", n)
    print("[+] size: ", n.bit_length(), "bits")

    # Calculate totient 'Phi(n)'
    phi = 1
    for k in primes_arr:
        phi *= (k - 1)

    # Calculate private key 'd'
    d = pow(config.e, -1, phi)

    # Generate Flag
    assert config.flag.startswith(b"CTF{")
    assert config.flag.endswith(b"}")
    enc_flag = bytes_to_long(config.flag)
    assert enc_flag < n

    # Encrypt Flag
    _enc = pow(enc_flag, config.e, n)

    with open ("flag.txt", "wb") as flag_file:
        flag_file.write(_enc.to_bytes(n.bit_length(), "little"))

    # Export RSA Key
    rsa = RSA.construct((n, config.e))
    with open ("public.pem", "w") as pub_file:
        pub_file.write(rsa.exportKey().decode())

LCG(線形合同法) は Xn+1 = (m*Xn + c) mod n の漸化式で生成される一連の乱数です。

初期値である seed は問題スクリプトにハードコードされていましたが、m,c,n の 3 つの値は与えられていません。

ただし、dump.txt として最初の 6 個の乱数が与えられています。

これらの値から何かしらの方法で m,c,n を特定して鍵生成に使用する素数列を特定できそうだったので、チームメンバーと相談しながら調べてみたところ、以下の記事がみつかりました。

参考：線形合同法 (Linear Congruential Generators) によって生成される擬似乱数を予測する - s4tt01237’s diary

どうやら LCG の使用する設定値は、出力結果の最初のいくつかがわかっていれば、生成された値の最大公約数から特定した法と、法を元にした連立方程式による演算で特定できるようです。

これを利用して、以下のスクリプトで m,c,n の 3 つの値を特定できました。

from Crypto.Util.number import inverse, GCD
from functools import reduce

prime_candidates = [2166771675595184069339107365908377157701164485820981409993925279512199123418374034275465590004848135946671454084220731645099286746251308323653144363063385,
6729272950467625456298454678219613090467254824679318993052294587570153424935267364971827277137521929202783621553421958533761123653824135472378133765236115,
2230396903302352921484704122705539403201050490164649102182798059926343096511158288867301614648471516723052092761312105117735046752506523136197227936190287,
4578847787736143756850823407168519112175260092601476810539830792656568747136604250146858111418705054138266193348169239751046779010474924367072989895377792,
7578332979479086546637469036948482551151240099803812235949997147892871097982293017256475189504447955147399405791875395450814297264039908361472603256921612,
2550420443270381003007873520763042837493244197616666667768397146110589301602119884836605418664463550865399026934848289084292975494312467018767881691302197]

def solve_unknown_increment(states, A, M):
    B = (states[1] - A * states[0]) % M
    return B

def solve_unknown_multiplier(states, M):
    A = (states[2] - states[1]) * inverse((states[1] - states[0]), M)
    return A

def solve_unknown_modulus(states):
    diffs = [X_1 - X_0 for X_0, X_1 in zip(states, states[1:])]
    multiples_of_M = [T_2 * T_0 - T_1 ** 2 for T_0, T_1, T_2, in zip(diffs, diffs[1:], diffs[2:])]

    # GCD(GCD(multiples_of_M[0],multiples_of_M[1]), multiples_of_M[2])
    M = reduce(GCD, multiples_of_M)
    return M

def test_unknown_modulus():
    M = solve_unknown_modulus(prime_candidates)
    M = solve_unknown_modulus(prime_candidates)
    A = solve_unknown_multiplier(prime_candidates, M)
    B = solve_unknown_increment(prime_candidates, A, M)

    print(M)
    print(A)
    print(B)

test_unknown_modulus()

これで、あとは e を特定することで Flag の復号に使用する秘密鍵の生成ができます。

e については、問題バイナリとして提供された RSA の公開鍵が 2048 bit RSA のサイズだったので、65537 を決め打ちました。

ここまでで特定した情報を元に以下のスクリプトを作成して Flag を復号できました。

import struct
from Crypto.PublicKey import RSA
from Crypto.Util.number import long_to_bytes, bytes_to_long, isPrime

class LCG:
    lcg_m = -6569199283741144524805092313800498379912765081239722709390321881123001934591054674566684669798886054155292305172680411106681470919005032801138448184653164447435662736622686458913807769346396147888409387744295360132038094168945987371927904880766531430748616858146076625544135687000281908879673294160897281532
    lcg_c = 3910539794193409979886870049869456815685040868312878537393070815966881265118275755165613835833103526090552456472867019296386475520134783987251699999776365
    lcg_n = 8311271273016946265169120092240227882013893131681882078655426814178920681968884651437107918874328518499850252591810409558783335118823692585959490215446923

    def __init__(self, lcg_s):
        self.state = lcg_s

    def next(self):
        self.state = (self.state * self.lcg_m + self.lcg_c) % self.lcg_n
        return self.state


if __name__ == '__main__':

    it = 8
    bits = 512

    # Find prime value of specified bits a specified amount of times
    seed = 211286818345627549183608678726370412218029639873054513839005340650674982169404937862395980568550063504804783328450267566224937880641772833325018028629959635
    lcg = LCG(seed)
    primes_arr = []
    items = 0
    primes_n = 1
    while True:
        for i in range(it):
            while True:
                prime_candidate = lcg.next()

                if not isPrime(prime_candidate):
                    continue
                elif prime_candidate.bit_length() != bits:
                    continue
                else:
                    primes_n *= prime_candidate
                    primes_arr.append(prime_candidate)
                    break
        
        # Check bit length
        if primes_n.bit_length() > 4096:
            # print("bit length", primes_n.bit_length())
            primes_arr.clear()
            primes_n = 1
            continue
        else:
            break
    
    # print(primes_arr)
    # print(len(primes_arr))

    # Create public key 'n'
    n = 1
    for j in primes_arr:
        n *= j
    # Calculate totient 'Phi(n)'
    phi = 1
    for k in primes_arr:
        phi *= (k - 1)

    # print("[+] n: ", n)
    # print("[+] size: ", n.bit_length(), "bits")
    # print("[+] phi: ", phi)

    rsa = RSA.construct((n, 65537))
    key = rsa.exportKey().decode()
    # print(key)

    d = pow(65537, -1, phi)
    # print("[+] d: ", d)

    with open("flag.txt", "rb") as f:
        data = f.read()
        c = int.from_bytes(data, "little")
        # print(c)

    # print(c)
    m = pow(c, d, n)
    flag = long_to_bytes(m)
    print(flag)

    # enc_flag = b'L\x13\x17\xea\x9e\x10\x13hy\x90kK\xdb? \xd5z7\t\xeb\xf3n\xf1\xd0\xc1\xad\x15\xf8ZN\x9c\xd9\xef\xbcz\xcc\xed\xd9:p\xf0\x1e\x97%T\xdb\xb0\'I\x17\x83mLi6\x1b\xd8 \x93%\xe9\xcd\x0f*\x9e\x1fJ\xb3\xb4\xeahnT\x92\xea<<\x159\xba\xb9vo\xf3\x9b\x8b\xf3\xe93?p\xad`\xd6\xa6T\x85m\x06\xd6\xb1\xd1\x8djQ\xe4\xf3Z\xf5\x10\xd7)G\x91\x13\x1c\xc6O\x0b8;\xed\x89\'\xf42\x92\x03\xa4\x80)y\x10\xdc\x0b;\x03\xf6\xff\x06C~;\xde\xf4\xf9\xd0\xd1\xcc\xfd\x10\x95\x9a\xa9\\\x91X{\xb6M\xe1d\xf4\xf57\xbd\x8a,\x07K\xd7B\x1c\xe5\xd1p=5\x01\x08\xb3\xafA\x00\xad\x90I\x1b\tdt\x9c\x08\xf2\xd2n\xd8%\x1e\xa4H\xb7G\xb5\xc1\tG$h\xa2\xe7z\xcf\xf9\xba\x17}\'&\x05\x1ecF\xc0\x86\xc7\xd9\xd1\r2!\xe1\xa1Z\xabp\xfe\x14C\xd0.+T\x87\x9dP\x17\xfc\xb6\x94\x98\x90q\xe3P\x1fPn\x07\xf1+;\xcc\xd3/\x0f\xde\x0eZL\xa7\xd5\xce\x1dF\x9c#\xdea\xcc,\xbe\xc0O\xb06\xbdi \xf9w\xa1\xac\x97\xfd\x93\x91c\xf5\xee\xd2U\xe32\xd7\xe8\xed\x90\xa4.Q\xca\xdc\x8btF<\xbb\xfe?\xdf\xf4\xfd\xde\xee^\xf3G\x8a\xb8<\xa0\x04U\xfb1>a:\xaf\xfb+\xf3\x10\x15\x9d\x04Md\x9c^\xda\xd3A\x14\x9eV\x05\xfd\xdcC\xa1\xf8\xb4\xf8\\\xb9\x89Bb?\x13\xf1s3\x98i\xb4e\x15\xa6@\xab\xbbR\x80\x1e\xd9\xb4\xd8U\xd6qC\xff\xff\xa7bFN\t\x0f\xa7|\xa1\x80r\xb6\xa5\xa8!\xbc\xe1\x08\xc2t\xe0\xa1\xc2"4%v\x91\xeeKg\x98E\x0e\xa4z\xb5\x01o\x9d\tS\x92\xf3\x1d\x1e\xa3\xe7\xce\xb99s`\x9ao"\xe2Z\xddg\x902\x12\x15\xd6N<\xebH2;\x93\x81`\xa39\x07\xc6\xc0%Wc\xf6\x82\x819\xe0\x99=\xc5\x9a\x95\x9bR\xf4>|@\xe6)\xf1L\x17\n\n\xa4\xac#d\xd9\x13\'\x16\xf9v\x02'
    # print(len(enc_flag))
    

    # text = b"myflag"
    # enc_flag = bytes_to_long(text)
    # _enc = pow(enc_flag, 65537, n)
    # with open ("myflag.txt", "wb") as flag_file:
    #     flag_file.write(_enc.to_bytes(n.bit_length(), "little"))
    # with open("myflag.txt", "rb") as f:
    #     data = f.read()
    #     number = int.from_bytes(data, "little")
    #     print(number)

    # m = pow(number, d, n)
    # flag = long_to_bytes(m)
    # print(flag)

PAPAPAPA(Misc)

Is this image really just white?

問題バイナリとして以下のような真っ白な JPEG が与えられます。

どうやらこの中に Flag が埋め込まれているようです。

white

当然ではありますが汎用ツールで解析を行っても Flag は取得できません。

バイトコードを走査してみてもそれらしい情報は見当たりませんでした。

また、このような画像の場合は LSB などが悪用されている場合も多いので以下のスクリプトで全ピクセルの RGB を抽出してみましたが、#FFFFFF 以外の色のピクセルは存在していませんでした。

from PIL import Image

def get_pixel_rgb(image_path):
    img = Image.open(image_path)
    pixels = img.load()
    width, height = img.size

    rgb_values = []
    for y in range(height):
        for x in range(width):
            r, g, b = pixels[x, y]
            rgb_values.append((r, g, b))

    return rgb_values

image_path = "white.jpg"
rgb_values = get_pixel_rgb(image_path)
for rgb in rgb_values:
    for px in rgb:
        if px != 255:
            print(rgb)

ここで若干手詰まりしましたが、試しに ImageMagick をかけてみたところ、画像のサイズが 512*512 であるにもかかわらず、sampling-factor が 3x1,3x1,3x1 になっていることに気づきました。

どうやらこの画像ではクロマサブサンプリングが使用されているようです。

./magick identify -verbose white.jpg
>
jpeg:colorspace: 2
jpeg:sampling-factor: 3x1,3x1,3x1

JPEG は、画像を小さな正方形の単位に分割し、それぞれの正方形の色と明るさを数式化することで圧縮して保存することができる方法です。

この時の正方形は 8*8 ピクセルと既定されています。つまり、本来 JPEG フォーマットの縦横サイズは常に 8 の倍数になります。

JPEG では、画像の解像度を下げてサイズを小さくするために、クロマサブサンプリングという技術を使用する場合があります。

クロマサブサンプリングは、人間の視覚が色よりも明るさに敏感であることを利用します。

具体的には、意図的に「色の情報」を「明るさの情報」よりも少なくすることで、画像の見た目(画質)を維持したまま画像ファイルを小さく(低解像度)に変換することができます。

クロマサブサンプリングは、一般的には 2x2 の比率らしいですが、今回は 3x1 に設定されていました。

JPEG でクロマサブサンプリングが行われている場合、JPEG の 1 ブロックのサイズは、基本の 8*8 に画像成分の中で最大のサンプリングファクタをかけた値になります。

つまり、今回は 24x8 がブロックサイズになるわけです。

参考：JPEG - Simple English Wikipedia, the free encyclopedia

参考：Chroma subsampling - Wikipedia

参考：画像データの構造

参考：Chroma subsampling in JPG compression

参考：JPEG の YCbCr について - awm-Tech

ここで、512*512 ピクセルの問題画像の幅が 24 の倍数になっていないことに気づきます。

クロマサブサンプリングを行っている画像で画像のサイズがブロックサイズの倍数にならない場合、あふれた部分はパディングとして扱われ、SOF(JPEG ファイルの種類や主要な情報が記録されているセグメント)に書かれる画像サイズはパディングを差し引いた値が強制されます。

これによってパディング部分が実際の表示画像から消えるわけです。

ちなみに、パディング部分に隠されている画像については普通にイメージビューアなどでサイズの拡大を行っても取得できません。

このような場合は、SOF 領域内で JPEG の画像サイズを指定しているバイト列を直接書き換えてあげます。

def modify_sof0_segment(jpeg_path, new_width, new_height):
    with open(jpeg_path, "rb") as file:
        jpeg_data = bytearray(file.read())

    # SOF0セグメントの位置を検索
    sof0_marker = b'\xff\xc0'
    sof0_start = jpeg_data.find(sof0_marker)

    # SOF0セグメントのパラメータの位置を検索して表示
    parameter_start = sof0_start + 5
    print("Original SOF0 width : {}".format(int.from_bytes(jpeg_data[parameter_start:parameter_start + 2],"big")))
    print("Original SOF0 height : {}".format(int.from_bytes(jpeg_data[parameter_start + 2:parameter_start + 4],"big")))

    # 新しい幅と高さをバイト列に変換
    new_width_bytes = new_width.to_bytes(2, byteorder='big')
    new_height_bytes = new_height.to_bytes(2, byteorder='big')

    # 幅と高さを置き換える
    jpeg_data[parameter_start:parameter_start + 2] = new_width_bytes
    jpeg_data[parameter_start + 2:parameter_start + 4] = new_height_bytes

    print("New SOF0 width : {}".format(int.from_bytes(jpeg_data[parameter_start:parameter_start + 2],"big")))
    print("New SOF0 height : {}".format(int.from_bytes(jpeg_data[parameter_start + 2:parameter_start + 4],"big")))

    # 変更後のJPEGファイルを保存
    modified_jpeg_path = "modified.jpg"
    with open(modified_jpeg_path, "wb") as file:
        file.write(jpeg_data)
        print("==> Saved new JPEG")

# 使用例
jpeg_path = "white.jpg"
new_width = 512
new_height = 528
modify_sof0_segment(jpeg_path, new_width, new_height)

最終的に上記の Solver を作成して画像の幅を 528 に変更することで、パディング部分に隠された Flag を取得することができました。

image-20230627213617828

まとめ

レベルアップを感じられるいい機会でした。

ただ、まだまだ上位は遠いので引き続き精進します。

Google CTF は公式 Writeup が丁寧でありがたいので、解けなかった問題はまたチャレンジしていきます。

参考：google/google-ctf: Google CTF

Published Jun 27, 2023

リバースエンジニアになりたいCTF Player(Team: 0nePadding)。WinDbgとYARAが好き。OSCP / CISSP / AtCoder 緑 Microsoft Japanに所属してます。発言はすべて個人の見解。かしわば on Twitter