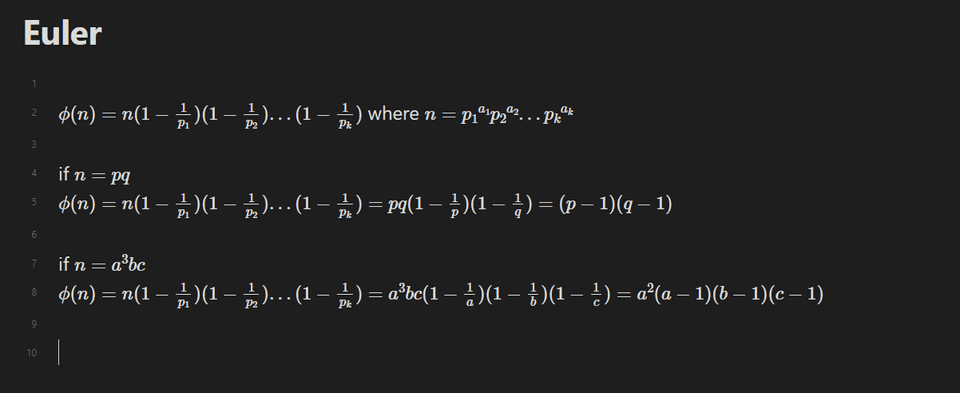2023 年 11 月 25 日から開催されていた Gracier CTF 2023 に 0nePadding で参加して 150 位でした。
今回は開催期間中にあまり時間が取れませんでしたが、簡単に Writeup を書きます。
もくじ
ARISAI(Crypto)
I heard that RSA with multiple primes is more secure. My N is very large, so there should not be a problem.
問題バイナリとして以下のコードと output.txt が与えられます。
from Crypto.Util.number import bytes_to_long
from Crypto.Util.number import getPrime
PRIME_LENGTH = 24
NUM_PRIMES = 256
FLAG = b"gctf{redacted}"
N = 1
e = 65537
for i in range(NUM_PRIMES):
prime = getPrime(PRIME_LENGTH)
N *= prime
ct = pow(bytes_to_long(FLAG), e, N)
print(f"{N=}")
print(f"{e=}")
print(f"{ct=}")N=1184908748889071774788034737775985521200704101703442353533571651469039119038363889871690290631780514392998940707556520304994251661487952739548636064794593979743960985105714178256254882281217858250862223543439960706396290227277478129176832127123978750828494876903409727762030036738239667368905104438928911566884429794089785359693581516505306703816625771477479791983463382338322851370493663626725244651132237909443116453288042969721313548822734328099261670264015661317332067465328436010383015204012585652642998962413149192518150858822735406696105372552184840669950255731733251466001814530877075818908809387881715924209232067963931299295012877100632316050826276879774867425832387424978221636157426227764972761357957047150626791204295493153062565652892972581618176577163744310556692610510074992218502075083140232623713873241177386817247671528165164472947992350655138814891455499972562301161585763970067635688236798480514440398603568227283629452476242623289661524243073929894099518473939222881149459574426407208658860251686137960952889074096311126991477096465624470265619377139983649503903820480974951491378311837933293607705488991162022547957926530402988912221198282579794590930661493745233069145707902854299501706154802038942258911515981663207152069613126155243024789689987554767962281273345273757236723762684230158310314189489269922058062081424352003908442430243686562569467793068370441732743572240164014190275463904986105758545036928880621165599686076511511089276388190078187849622221351011692443859919384379432387437072419707649486293684966456033518855679391672980173280496419686363359529398834403906418139786395934302273747490127295066208248715874656180233559644161531014137838623558729789331274400542717269108353265885948166102045041669627782992845494987948783304254174326130201166965174477449798721151991240203641
e=65537
ct=268829805459609475588440899873097740407996768854076329496002425282199615879909227647380967635165606878898541606457683227761652305836586321855100255485305118037701500609605019785162541750877335573032359895573772603246111506991979320486028250721513277767642375361127152574528694298160906073442383962020636918610527024050576972769852306021296823499884948279413653216802756618690182635446020844210831886652986287932378470425746444631963933610367607515800649608436183004088441881238148504635598468243968695248287570279766119573944421327504565309861792437849662128566261080923059583840204287527201636471106753069738472306223410300379312983945939043519755909420737707495224846116170095923898104488099329762265149868062693687303917610957104520999978944379566136253252697346935036425206126213766976582551430726756840294537354912787885103742021813054656962241068550049435394355553796824094853195888610994254949530524531633088750916669188277025883371307926545593346345011181011886157628805587723572874545440223921942144548540109099572715194182349314576321627183804149379561322969725485272107142991680959335537127382716195040449341448266408777436145121388591741613272241408064729715121476227737259932422493622000014673154665474739974557976672498027364986075870354093242809763072555932073688776712239151696700128393589329790478951588551070833013708885416360627613835550721939073618725634813608997025047929327270234611128029339388251117036658410438813874667672407000490721438737857471847655487642835059784967516451098631494261100960513521722400650533821661854325599281416744189966724295645707952292786069145361070873245192529272080607536319284389065418040578100669665069777133031446812281199863684982910055858515634879595144557407925298026899908970790756383369461817536923660051327566555421265363733995050644914554395836353253513与えられた Python スクリプトを読むと、24 bit の素数を 256 個かけ合わせた数を n として Flag を RSA 暗号化したものが output.txt の ct であることがわかります。
256 個の素数をかけ合わせた n は非常に大きいものの、使用する素数は 24 bit ですので簡単に素因数分解ができます。
今回は適当にインターネット上で見つけた素数表を先頭から mod を取っていくことですべての構成要素となる素数を特定しました。
素因数分解に成功したところで、phi の作成に少々手間取りました。
この問題のような multi-prime RSA の場合、オイラー関数の定義は以下のようになるようです。
取得した素数のバケットを取ってみると (8725153,11369903,16177433) の 3 つの素数がそれぞれ 2 つずつ使用されてることがわかりました。
そのため、重複している素数のみ p * (p-1) のような演算を行うことで phi を取得し、復号に成功しました。
以下の Solver で Flag を取得できました。
from Crypto.Util.number import long_to_bytes, bytes_to_long
n=1184908748889071774788034737775985521200704101703442353533571651469039119038363889871690290631780514392998940707556520304994251661487952739548636064794593979743960985105714178256254882281217858250862223543439960706396290227277478129176832127123978750828494876903409727762030036738239667368905104438928911566884429794089785359693581516505306703816625771477479791983463382338322851370493663626725244651132237909443116453288042969721313548822734328099261670264015661317332067465328436010383015204012585652642998962413149192518150858822735406696105372552184840669950255731733251466001814530877075818908809387881715924209232067963931299295012877100632316050826276879774867425832387424978221636157426227764972761357957047150626791204295493153062565652892972581618176577163744310556692610510074992218502075083140232623713873241177386817247671528165164472947992350655138814891455499972562301161585763970067635688236798480514440398603568227283629452476242623289661524243073929894099518473939222881149459574426407208658860251686137960952889074096311126991477096465624470265619377139983649503903820480974951491378311837933293607705488991162022547957926530402988912221198282579794590930661493745233069145707902854299501706154802038942258911515981663207152069613126155243024789689987554767962281273345273757236723762684230158310314189489269922058062081424352003908442430243686562569467793068370441732743572240164014190275463904986105758545036928880621165599686076511511089276388190078187849622221351011692443859919384379432387437072419707649486293684966456033518855679391672980173280496419686363359529398834403906418139786395934302273747490127295066208248715874656180233559644161531014137838623558729789331274400542717269108353265885948166102045041669627782992845494987948783304254174326130201166965174477449798721151991240203641
e=65537
c=268829805459609475588440899873097740407996768854076329496002425282199615879909227647380967635165606878898541606457683227761652305836586321855100255485305118037701500609605019785162541750877335573032359895573772603246111506991979320486028250721513277767642375361127152574528694298160906073442383962020636918610527024050576972769852306021296823499884948279413653216802756618690182635446020844210831886652986287932378470425746444631963933610367607515800649608436183004088441881238148504635598468243968695248287570279766119573944421327504565309861792437849662128566261080923059583840204287527201636471106753069738472306223410300379312983945939043519755909420737707495224846116170095923898104488099329762265149868062693687303917610957104520999978944379566136253252697346935036425206126213766976582551430726756840294537354912787885103742021813054656962241068550049435394355553796824094853195888610994254949530524531633088750916669188277025883371307926545593346345011181011886157628805587723572874545440223921942144548540109099572715194182349314576321627183804149379561322969725485272107142991680959335537127382716195040449341448266408777436145121388591741613272241408064729715121476227737259932422493622000014673154665474739974557976672498027364986075870354093242809763072555932073688776712239151696700128393589329790478951588551070833013708885416360627613835550721939073618725634813608997025047929327270234611128029339388251117036658410438813874667672407000490721438737857471847655487642835059784967516451098631494261100960513521722400650533821661854325599281416744189966724295645707952292786069145361070873245192529272080607536319284389065418040578100669665069777133031446812281199863684982910055858515634879595144557407925298026899908970790756383369461817536923660051327566555421265363733995050644914554395836353253513
primes = [8441831, 8450987, 8452019, 8473027, 8476817, 8523661, 8525711, 8608673, 8633423, 8641453, 8725153, 8725153, 8786017, 8796721, 8824679, 8850601, 8913481, 8933437, 9016037, 9041551, 9075889, 9095939, 9126197, 9142547, 9163981, 9172531, 9196001, 9223867, 9253319, 9265309, 9277921, 9298747, 9300803, 9357883, 9368759, 9405353, 9444839, 9552029, 9569057, 9584371, 9663629, 9696719, 9720223, 9748049, 9770723, 9801269, 9828727, 9836483, 9838117, 9853043, 9873373, 9883469, 9884603, 9905167, 9989579, 10000759, 10064897, 10114409, 10122389, 10213001, 10214591, 10228861, 10235447, 10344643, 10428001, 10433911, 10438013, 10441523, 10476001, 10514083, 10523977, 10605817, 10650929, 10667479, 10699517, 10731407, 10732091, 10754837, 10773781, 10849837, 10861127, 10893173, 10918459, 10943417, 10944433, 11028001, 11049739, 11057621, 11073793, 11084419, 11113789, 11152859, 11156681, 11230451, 11239903, 11369903, 11369903, 11462177, 11470343, 11504419, 11519971, 11543971, 11559637, 11625619, 11633267, 11661121, 11768401, 11847721, 11909747, 11915809, 11925691, 11928173, 11945093, 11990089, 12010259, 12089663, 12109277, 12231853, 12240667, 12274813, 12319117, 12339689, 12350357, 12358079, 12387329, 12407609, 12407959, 12515033, 12550357, 12599803, 12621067, 12652597, 12705883, 12804707, 12808151, 12824027, 12932669, 12967831, 13046717, 13059269, 13076249, 13128433, 13170671, 13202297, 13227367, 13328803, 13366687, 13371181, 13415921, 13417357, 13424921, 13430423, 13534007, 13561657, 13566431, 13568981, 13587683, 13625263, 13653811, 13655797, 13669967, 13673927, 13755149, 13799299, 13823059, 13865617, 13870601, 13997617, 14013617, 14044937, 14046449, 14086979, 14103413, 14162843, 14217041, 14311291, 14339863, 14340289, 14377679, 14407667, 14423561, 14435203, 14465153, 14466281, 14475521, 14482381, 14535811, 14548939, 14549063, 14588369, 14624459, 14633851, 14650763, 14693927, 14713939, 14738869, 14797501, 14880347, 14910199, 14922409, 14982181, 15005579, 15020413, 15031937, 15103373, 15181499, 15185399, 15209617, 15232961, 15299831, 15365261, 15441739, 15459343, 15470893, 15475193, 15489707, 15501071, 15682181, 15689647, 15689981, 15707093, 15707143, 15748631, 15792169, 15793247, 15798877, 15922301, 15947639, 16032721, 16045049, 16071229, 16080319, 16175597, 16177433, 16177433, 16198717, 16199101, 16212913, 16225283, 16254883, 16312763, 16336267, 16359283, 16405027, 16432721, 16497373, 16593167, 16594681, 16629163, 16632713, 16643707, 16657153, 16679137, 16701907, 16738913, 16755269]
phi = 1
t = 1
# https://crypto.stackexchange.com/questions/74891/decrypting-multi-prime-rsa-with-e-n-and-factors-of-n-given
set(primes)
for p in primes:
t *= p
if p in (8725153,11369903,16177433):
phi = phi * p * (p-1)
else:
phi *= (p-1)
assert(t == n)
d = pow(e,-1,phi)
long_to_bytes(pow(c,d,n))
# gctf{maybe_I_should_have_used_bigger_primes}SOP(Rev)
I am sure you know OOP, but do you also know SOP?
問題バイナリとして与えられた ELF ファイルを Ghidra でデコンパイルしてみると以下の main 関数を特定できます。
bool main(void)
{
size_t sVar1;
ssize_t sVar2;
sVar1 = strlen(&DAT_000060f0);
DAT_000061c8 = (int)sVar1;
if (DAT_000061c8 == 0) {
sVar2 = read(0,&DAT_000060f0,0x44);
DAT_000061c8 = (int)sVar2;
}
return DAT_000061c8 != 0x44;
}しかし、このコードは標準入力を DAT_000060f0 に格納し、そのサイズが 0x44 に一致したかどうかを戻り値として返す関数になっており、正直何をしているかよくわかりません。
とりあえず試しに 0x44 の入力値を与えてプログラムを実行してみたところ、FAIL という文字列が出力されました。
そこで、Ghidra で FAIL という文字列から逆引きを行ったところ、以下の処理を行っている関数を見つけることができました。
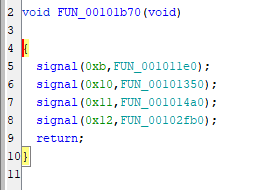
この関数自体は、以下の箇所で signal(0x16,Check); のように未定義のシグナル 0x16 のコールバック関数として定義されていることがわかりました。
参考:signal.h
また、この関数では同時に 0xe と 0x15 のシグナルが定義されています。
0xe のシグナルのコールバック関数では 0x15 が raise され、0x15 のシグナルのコールバックで 0x16 が raise されます。
つまり、どこかで SIGTERM が呼び出されたところから一連の処理が行われて、最後に Flag の検証が行われているという推測が立ちます。
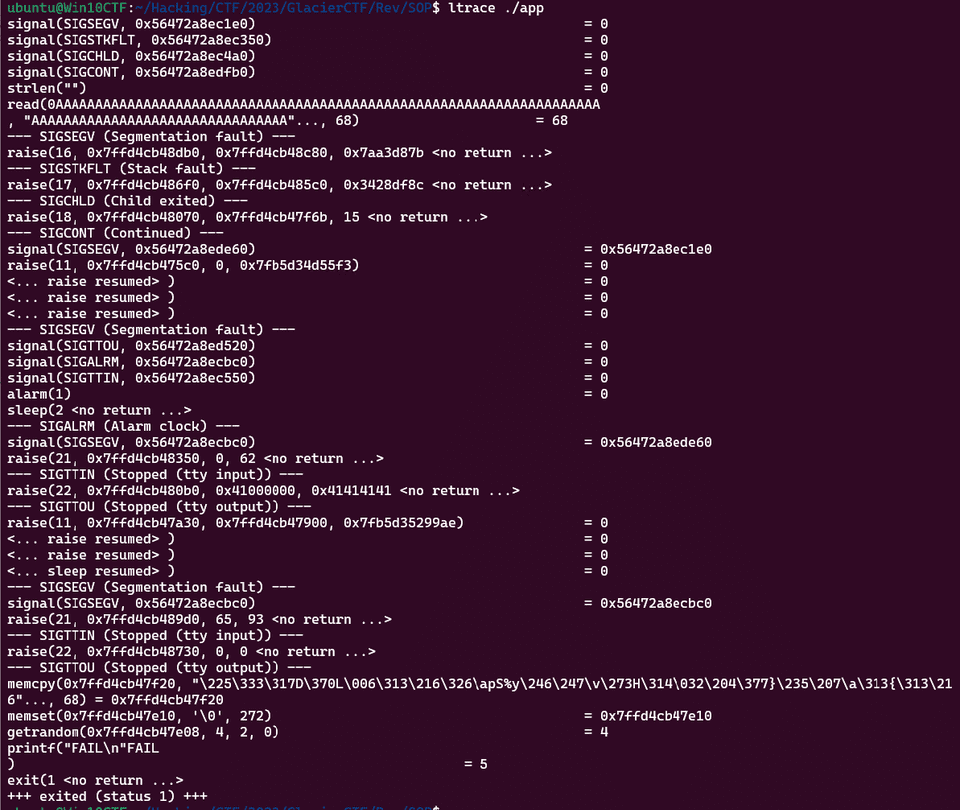
このあたりの一連の処理は gdb を噛ませていると上手く追うことができなかったので ltrace を使用しました。
すると、以下のように SIGSEGV から始まって複数のシグナルを経由した後、最後に FAIL が出力される挙動を追うことができました。
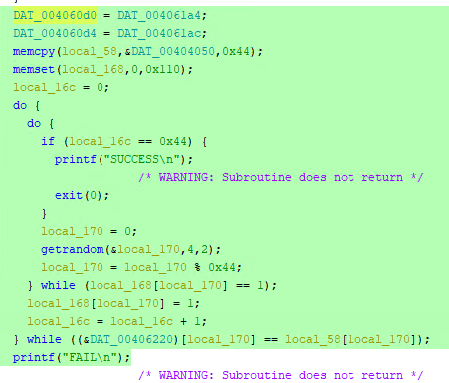
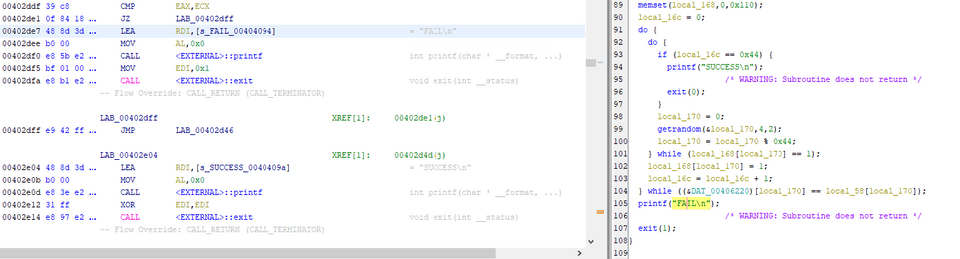
さて、ここで細かい実装はわかりませんが、最後の行で (&DAT_00406220)[local_170] == local_58[local_170] が一致するかを比較していることがわかります。
local58 には DAT00404050 に定義されている 0x44 バイト分のバイト列が格納されます。
つまり、最終的に入力値を変換した DAT00406220 が DAT00404050 のバイト列と一致するような入力が Flag になりそうだということがわかります。
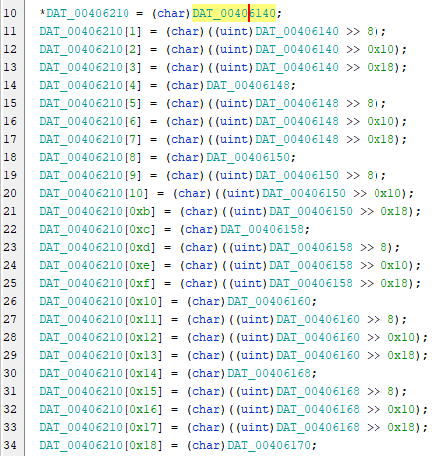
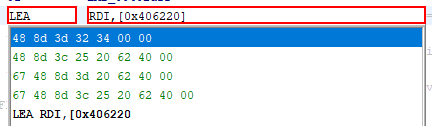
ここでコードを少しさかのぼると、DAT00406220 を含む領域に書き込まれる値は、DAT00406140 以降の領域から取得した値であることがわかります。
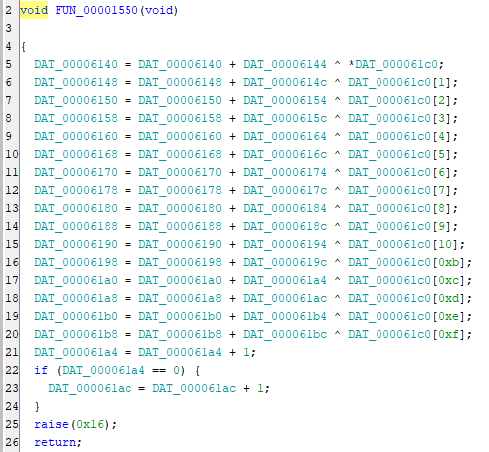
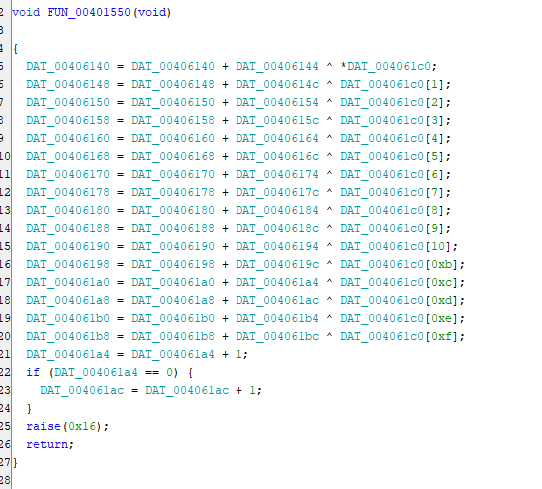
さらにこの領域へのアクセスをさかのぼると、以下の箇所で各バイト値に対して XOR を繰り返していることがわかります。
DAT_00406140 以降の領域の初期値は空のようです。
そのため、この時点で詳細は不明ですが、何らかのキーを元に Flag を XOR した結果が DAT_00404050 のバイト列に一致するのではないかという推測が立ちます。
これを確かめるため、最終的に入力値を変換した DAT_00406220 に格納される情報を参照することにします。
gdb は上手く動作しないため、FAIL が出力される printf 関数の引数を書き換えることで、DAT_00406220 に格納される情報を参照します。(Frida を使う方が楽かもしれません)
実際の書き換えは以下のように行いました。
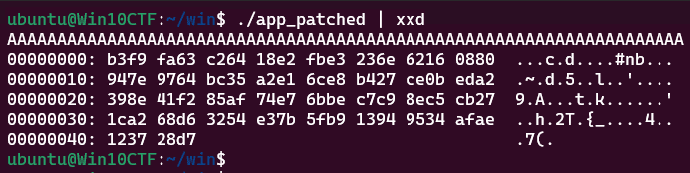
ここでパッチしたプログラムに 0x44 バイト分の A を入力として与えると以下のように DAT_00406220 に格納されるバイト列が出力されます。
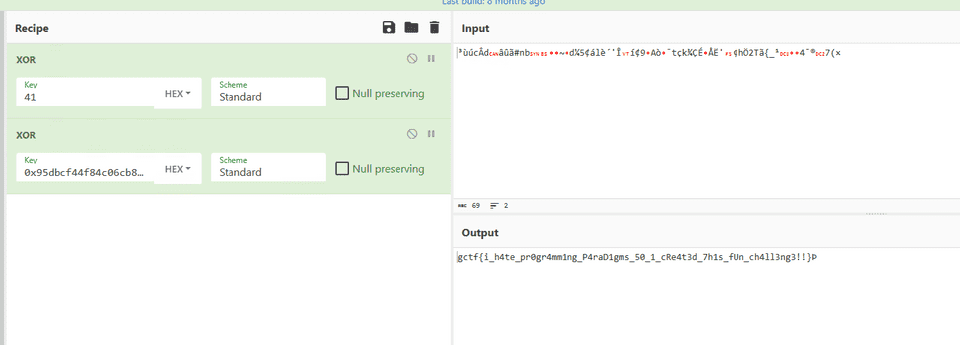
ここで取得できたバイト列を A で XOR してキーを復元し、さらに DAT_00404050 にハードコードされているバイト列と XOR を行ったところ、以下のように正しい Flag を取得することができました。
まとめ
SOP は非常に面白い問題でした。
バイナリを動的解析できれば簡単に解ける問題ですが、シグナルによって各処理が呼び出されているせいか、gdb などのデバッガで上手く解析することができません。
恐らく想定解は Frida などでシグナルをフックしながら動的解析を進めることではないかと思うので、別解も試してみたいと思います。