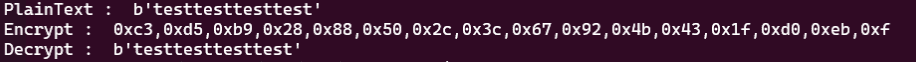もくじ
先日参加した WMCTF の問題で AES の実装を見抜けなかったり自力で復号スクリプトを作成できなかったりといった課題に直面したので、AES(Rijndael) の実装について少し腰を据えて学んでみることにしました。
参考:Android のネイティブライブラリ関数解析と RC4 と AES の復号を行う【WMCTF 2023】 - かえるのひみつきち
AES の復号が必要な Rev の問題は今までも何度か出ていたのですが、特定した Key と IV から Cyberchef で簡単で復号できるものしか解けたことがなく、Rijndael SBox を特定して復号スクリプトを作成するような問題は解けずに終わっていたので、これを機に少しでも解けるようにしていきたいと思います。
参考情報
参考:FIPS 197 AES
参考:[暗号入門] 実装して理解する AES - YouTube
参考:AES Encryption & Decryption In Python: Implementation, Modes & Key Management
AES(Rijndael) の概要
現在、安全な暗号化アルゴリズムとしての AES は、一般的に Rijndael と呼ばれるアルゴリズムを意味します。
この AES はデータの暗号化と復号に同じキーを利用する対称暗号です。
AES は、鍵の総当たりが計算量的に困難であることで安全性が担保されており、AES-256 のように、鍵の長さが長くなる方が安全性が高いと言えます。
AES による暗号化を行う場合、まず 128, 192, 256, 512 bit のいずれかの長さのキーを用意します。
多くの場合には、256 bit(Base64 エンコードした場合に 44 文字) の鍵を利用する AES-256 が使用されるようです。
Cipher と Inverse Cipher
AES では、暗号化の処理を Cipher、復号の処理を Inverse Cipher と呼び、それぞれ以下の疑似コードで表現しています。
Cipher(byte in[4*Nb], byte out[4*Nb], word w[Nb*(Nr+1)])
begin
byte state[4,Nb]
state = in
AddRoundKey(state, w[0, Nb-1]) // See Sec. 5.1.4
for round = 1 step 1 to Nr–1
SubBytes(state) // See Sec. 5.1.1
ShiftRows(state) // See Sec. 5.1.2
MixColumns(state) // See Sec. 5.1.3
AddRoundKey(state, w[round*Nb, (round+1)*Nb-1])
end for
SubBytes(state)
ShiftRows(state)
AddRoundKey(state, w[Nr*Nb, (Nr+1)*Nb-1])
out = state
end復号を行う Inverse Cipher は、Cipher の逆順の処理を行います。
InvCipher(byte in[4*Nb], byte out[4*Nb], word w[Nb*(Nr+1)])
begin
byte state[4,Nb]
state = in
AddRoundKey(state, w[Nr*Nb, (Nr+1)*Nb-1]) // See Sec. 5.1.4
for round = Nr-1 step -1 downto 1
InvShiftRows(state) // See Sec. 5.3.1
InvSubBytes(state) // See Sec. 5.3.2
AddRoundKey(state, w[round*Nb, (round+1)*Nb-1])
InvMixColumns(state) // See Sec. 5.3.3
end for
InvShiftRows(state)
InvSubBytes(state)
AddRoundKey(state, w[0, Nb-1])
out = state
end以下で各項目を読み解いていきます。
Key-Block-Round の指定
とりあえず、[暗号入門] 実装して理解する AES - YouTube を見つつ FIPS 197 AES の Algorithm Specification の記載を読んでいきます。
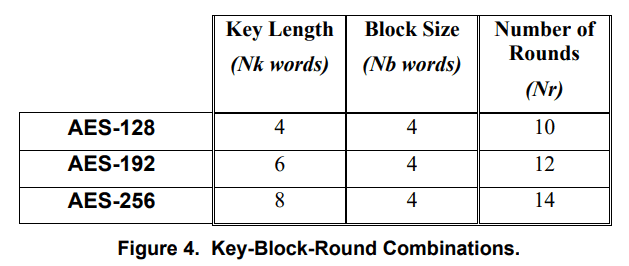
まず、AES のアルゴリズムでは、暗号化もしくは復号するデータ(input block)、暗号化された、もしくは復号されたデータ(output block)、そして処理中のデータ( State) の 3 つの長さが Nb = 4 として表されており、AES-128、192、256 の各アルゴリズムで共通です。
次に、AES のアルゴリズムでは、Cipher Key の長さは Nk で表現され、AES-128 の場合は 4、AES-256 の場合は 6 が指定されます。
最後に、アルゴリズムの実行回数を示すラウンド数は Nr で表現され、AES-128 の場合は 10、AES-256 の場合は 12 が指定されます。
FIPS 197 AES では、これらの組み合わせを以下の表でまとめています。
SBox について
Rev をやっているとよく見かけるのがこの SBox ですが、これは Cipher 関数の SubBytes で利用される 16 * 16 のバイト列です。
同様に、暗号化テキストの復号時には Inverse SBox を InvSubBytes 関数内で使用します。
SBox 自体は単なるバイト列ですので、詳しい用途については SubBytes や InvSubBytes の項で見ていきます。
ちなみに、以下の WIkipedia に記載の通り、通常は SBox と Inverse SBox のバイト列は既定値が存在しているっぽいです。
Inverse SBox は、既定の SBox に対して特別な演算を行った結果のバイト列になります。
SBox から Inverse SBox を求める演算は以下の Python スクリプトの通りです。
sbox = [ 0x63, 0x7c, 0x77, 0x7b, 0xf2, 0x6b, 0x6f, 0xc5, 0x30, 0x01, 0x67, 0x2b, 0xfe, 0xd7, 0xab, 0x76, 0xca, 0x82, 0xc9, 0x7d, 0xfa, 0x59, 0x47, 0xf0, 0xad, 0xd4, 0xa2, 0xaf, 0x9c, 0xa4, 0x72, 0xc0, 0xb7, 0xfd, 0x93, 0x26, 0x36, 0x3f, 0xf7, 0xcc, 0x34, 0xa5, 0xe5, 0xf1, 0x71, 0xd8, 0x31, 0x15, 0x04, 0xc7, 0x23, 0xc3, 0x18, 0x96, 0x05, 0x9a, 0x07, 0x12, 0x80, 0xe2, 0xeb, 0x27, 0xb2, 0x75, 0x09, 0x83, 0x2c, 0x1a, 0x1b, 0x6e, 0x5a, 0xa0, 0x52, 0x3b, 0xd6, 0xb3, 0x29, 0xe3, 0x2f, 0x84, 0x53, 0xd1, 0x00, 0xed, 0x20, 0xfc, 0xb1, 0x5b, 0x6a, 0xcb, 0xbe, 0x39, 0x4a, 0x4c, 0x58, 0xcf, 0xd0, 0xef, 0xaa, 0xfb, 0x43, 0x4d, 0x33, 0x85, 0x45, 0xf9, 0x02, 0x7f, 0x50, 0x3c, 0x9f, 0xa8, 0x51, 0xa3, 0x40, 0x8f, 0x92, 0x9d, 0x38, 0xf5, 0xbc, 0xb6, 0xda, 0x21, 0x10, 0xff, 0xf3, 0xd2, 0xcd, 0x0c, 0x13, 0xec, 0x5f, 0x97, 0x44, 0x17, 0xc4, 0xa7, 0x7e, 0x3d, 0x64, 0x5d, 0x19, 0x73, 0x60, 0x81, 0x4f, 0xdc, 0x22, 0x2a, 0x90, 0x88, 0x46, 0xee, 0xb8, 0x14, 0xde, 0x5e, 0x0b, 0xdb, 0xe0, 0x32, 0x3a, 0x0a, 0x49, 0x06, 0x24, 0x5c, 0xc2, 0xd3, 0xac, 0x62, 0x91, 0x95, 0xe4, 0x79, 0xe7, 0xc8, 0x37, 0x6d, 0x8d, 0xd5, 0x4e, 0xa9, 0x6c, 0x56, 0xf4, 0xea, 0x65, 0x7a, 0xae, 0x08, 0xba, 0x78, 0x25, 0x2e, 0x1c, 0xa6, 0xb4, 0xc6, 0xe8, 0xdd, 0x74, 0x1f, 0x4b, 0xbd, 0x8b, 0x8a, 0x70, 0x3e, 0xb5, 0x66, 0x48, 0x03, 0xf6, 0x0e, 0x61, 0x35, 0x57, 0xb9, 0x86, 0xc1, 0x1d, 0x9e, 0xe1, 0xf8, 0x98, 0x11, 0x69, 0xd9, 0x8e, 0x94, 0x9b, 0x1e, 0x87, 0xe9, 0xce, 0x55, 0x28, 0xdf, 0x8c, 0xa1, 0x89, 0x0d, 0xbf, 0xe6, 0x42, 0x68, 0x41, 0x99, 0x2d, 0x0f, 0xb0, 0x54, 0xbb, 0x16 ]
inverse_sbox = [0] * 256
for i in range(256):
line = (sbox[i] & 0xf0) >> 4
rol = sbox[i] & 0xf
inverse_sbox[(line * 16) + rol] = i
for i in range(len(inverse_sbox)):
if (i % 16 == 0):
print("")
print("0x%02X"%inverse_sbox[i],end=",")
print("")実際に既定値(?) の SBox を与えて実行すると、Wikipedia のページに記載の Inverse SBox と同じバイト列を得ることができます。
$ python3 sample.py
>
0x52,0x09,0x6A,0xD5,0x30,0x36,0xA5,0x38,0xBF,0x40,0xA3,0x9E,0x81,0xF3,0xD7,0xFB,
0x7C,0xE3,0x39,0x82,0x9B,0x2F,0xFF,0x87,0x34,0x8E,0x43,0x44,0xC4,0xDE,0xE9,0xCB,
0x54,0x7B,0x94,0x32,0xA6,0xC2,0x23,0x3D,0xEE,0x4C,0x95,0x0B,0x42,0xFA,0xC3,0x4E,
0x08,0x2E,0xA1,0x66,0x28,0xD9,0x24,0xB2,0x76,0x5B,0xA2,0x49,0x6D,0x8B,0xD1,0x25,
0x72,0xF8,0xF6,0x64,0x86,0x68,0x98,0x16,0xD4,0xA4,0x5C,0xCC,0x5D,0x65,0xB6,0x92,
0x6C,0x70,0x48,0x50,0xFD,0xED,0xB9,0xDA,0x5E,0x15,0x46,0x57,0xA7,0x8D,0x9D,0x84,
0x90,0xD8,0xAB,0x00,0x8C,0xBC,0xD3,0x0A,0xF7,0xE4,0x58,0x05,0xB8,0xB3,0x45,0x06,
0xD0,0x2C,0x1E,0x8F,0xCA,0x3F,0x0F,0x02,0xC1,0xAF,0xBD,0x03,0x01,0x13,0x8A,0x6B,
0x3A,0x91,0x11,0x41,0x4F,0x67,0xDC,0xEA,0x97,0xF2,0xCF,0xCE,0xF0,0xB4,0xE6,0x73,
0x96,0xAC,0x74,0x22,0xE7,0xAD,0x35,0x85,0xE2,0xF9,0x37,0xE8,0x1C,0x75,0xDF,0x6E,
0x47,0xF1,0x1A,0x71,0x1D,0x29,0xC5,0x89,0x6F,0xB7,0x62,0x0E,0xAA,0x18,0xBE,0x1B,
0xFC,0x56,0x3E,0x4B,0xC6,0xD2,0x79,0x20,0x9A,0xDB,0xC0,0xFE,0x78,0xCD,0x5A,0xF4,
0x1F,0xDD,0xA8,0x33,0x88,0x07,0xC7,0x31,0xB1,0x12,0x10,0x59,0x27,0x80,0xEC,0x5F,
0x60,0x51,0x7F,0xA9,0x19,0xB5,0x4A,0x0D,0x2D,0xE5,0x7A,0x9F,0x93,0xC9,0x9C,0xEF,
0xA0,0xE0,0x3B,0x4D,0xAE,0x2A,0xF5,0xB0,0xC8,0xEB,0xBB,0x3C,0x83,0x53,0x99,0x61,
0x17,0x2B,0x04,0x7E,0xBA,0x77,0xD6,0x26,0xE1,0x69,0x14,0x63,0x55,0x21,0x0C,0x7DAndroid のネイティブライブラリ関数解析と RC4 と AES の復号を行う【WMCTF 2023】 - かえるのひみつきち で解いた問題のように、SBox のバイト列がバイナリ内で Swap されるなどの加工が行われる場合や、そもそもカスタム SBox を利用している場合などには、復号に使用する Inverse SBox を取得するためにも、上記のスクリプトの実行が必要となりそうです。
SubBytes 関数について
SubBytes 関数は、置換テーブルである SBox を使用して、State の各バイトの変換(?) を行う関数のようです。
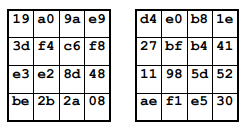
SubBytes がどのようにして入力値を変換していくのかについては、Appendix B – Cipher Example の項が参考になりました。
ここでは、入力値 input を 4 バイトごとのブロック単位に分割して、SBox を利用して変換を行った際の遷移が例示されます。
SubBytes 関数の実装の詳細については、[暗号入門] 実装して理解する AES の動画の 13 分あたりの内容が参考になりました。
ShiftRows 関数について
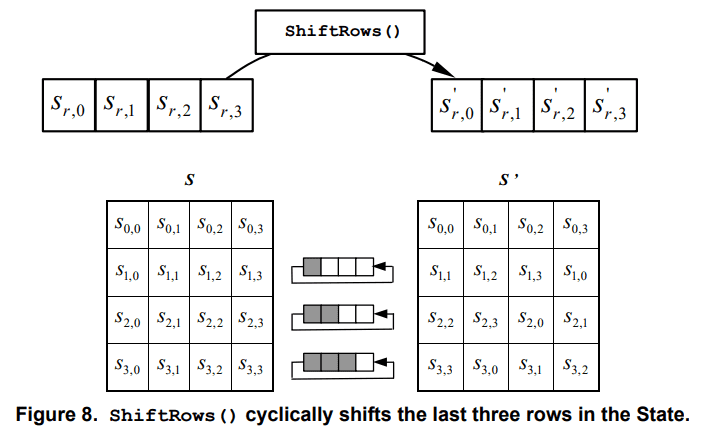
ShiftRows 関数は、Cipher 内の各ラウンドの処理にて、SubBytes の次に呼び出される関数です。
この処理は比較的シンプルで、State(?) の各列ごとに左にローテして、あふれたバイトは右側に循環ささせるような処理を実施するようです。
Appendix の例示でも、バイト値の移動を確認することができます。
MixColumns 関数について
ラウンドの処理にて、ShiftRows の次に呼び出される関数が MixColumns です。
MixColumns では、係数付きの多項式と State の乗算を行う関数らしいです。
(理解が怪しいので詳細は FIPS 197 AES を参照してください。)
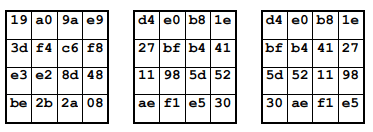
Appendix で例示されている MixColumns を実行した後の State の遷移は以下の通りです。
[暗号入門] 実装して理解する AES - YouTube の動画だと 16 分あたりから解説がありました。
AddRoundKey 関数について
AddRoundKey 関数は、以下の Cipher の疑似コードからわかる通り、ラウンドの開始前と、ラウンドの最後、そして Cipher の終わりに呼ばれる関数のようです。
Cipher(byte in[4*Nb], byte out[4*Nb], word w[Nb*(Nr+1)])
begin
byte state[4,Nb]
state = in
AddRoundKey(state, w[0, Nb-1]) // See Sec. 5.1.4
for round = 1 step 1 to Nr–1
SubBytes(state) // See Sec. 5.1.1
ShiftRows(state) // See Sec. 5.1.2
MixColumns(state) // See Sec. 5.1.3
AddRoundKey(state, w[round*Nb, (round+1)*Nb-1])
end for
SubBytes(state)
ShiftRows(state)
AddRoundKey(state, w[Nr*Nb, (Nr+1)*Nb-1])
out = state
endAddRoundKey 関数は、XOR を使用して State に Round Key を追加する変換に利用する関数です。
Round Key の長さは State のサイズに等しく、Nb = 4 の場合には 128 bit(16 Byte) になるようです。
AES による暗号化と復号を試してみる
ここまでで AES の Cipher 内で行われる処理のイメージを把握することができたので、実際に暗号化と復号を試してみようと思います。
AES のロジックを自分で実装するのは今回の趣旨ではないので普通に Github で入手してきたサンプルコードを利用させてもらいます。
参考:kokke/tiny-AES-c: Small portable AES128/192/256 in C
まずは、上記のリポジトリから tiny-AES-c のソースコードを Fork したリポジトリのコードをダウンロードし、make コマンドで test.elf をビルドしてみます。
git clone https://github.com/kash1064/tiny-AES-c
cd tiny-AES-c
make clean && make AES256=1 && ./test.elfビルド時に暗号化アルゴリズムを AES-256 に指定しています。
もとのリポジトリのソースコードを見てみると、sbox と rsbox 、そして AES の Key や PlainText がそれぞれハードコードされていることがわかります。
僕の Fork しているソースコードの方では、任意の Key と Plain Text のバイト列をコーディングして暗号化と復号を試せるようにしています。
任意の入力を埋め込む場合は、test.c の以下のコードを編集します。
static int encrypt_ecb(void)
{
#if defined(AES256)
uint8_t key[] = { 0x60, 0x3d, 0xeb, 0x10, 0x15, 0xca, 0x71, 0xbe, 0x2b, 0x73, 0xae, 0xf0, 0x85, 0x7d, 0x77, 0x81, 0x1f, 0x35, 0x2c, 0x07, 0x3b, 0x61, 0x08, 0xd7, 0x2d, 0x98, 0x10, 0xa3, 0x09, 0x14, 0xdf, 0xf4 };
#elif defined(AES192)
uint8_t key[] = { 0x8e, 0x73, 0xb0, 0xf7, 0xda, 0x0e, 0x64, 0x52, 0xc8, 0x10, 0xf3, 0x2b, 0x80, 0x90, 0x79, 0xe5, 0x62, 0xf8, 0xea, 0xd2, 0x52, 0x2c, 0x6b, 0x7b };
#elif defined(AES128)
uint8_t key[] = { 0x2b, 0x7e, 0x15, 0x16, 0x28, 0xae, 0xd2, 0xa6, 0xab, 0xf7, 0x15, 0x88, 0x09, 0xcf, 0x4f, 0x3c };
#endif
// 16 バイトの倍数
// ",".join([hex(ord(c)) for c in "testtesttesttest"])
uint8_t in[] = { 0x74,0x65,0x73,0x74,0x74,0x65,0x73,0x74,0x74,0x65,0x73,0x74,0x74,0x65,0x73,0x74 };
struct AES_ctx ctx;
printf("Plain Text:\n");
for (int i = 0; i < sizeof(in) / sizeof(in[0]); i++)
{
printf("0x%02x, ", in[i]);
}
printf("\n");
AES_init_ctx(&ctx, key);
AES_ECB_encrypt(&ctx, in);
printf("ECB encrypt:\n");
for (int i = 0; i < sizeof(in) / sizeof(in[0]); i++)
{
printf("0x%02x, ", in[i]);
}
printf("\n");
return(0);
}
static int decrypt_ecb(void)
{
#if defined(AES256)
uint8_t key[] = { 0x60, 0x3d, 0xeb, 0x10, 0x15, 0xca, 0x71, 0xbe, 0x2b, 0x73, 0xae, 0xf0, 0x85, 0x7d, 0x77, 0x81, 0x1f, 0x35, 0x2c, 0x07, 0x3b, 0x61, 0x08, 0xd7, 0x2d, 0x98, 0x10, 0xa3, 0x09, 0x14, 0xdf, 0xf4 };
uint8_t in[] = { 0xc3, 0xd5, 0xb9, 0x28, 0x88, 0x50, 0x2c, 0x3c, 0x67, 0x92, 0x4b, 0x43, 0x1f, 0xd0, 0xeb, 0x0f };
#elif defined(AES192)
uint8_t key[] = { 0x8e, 0x73, 0xb0, 0xf7, 0xda, 0x0e, 0x64, 0x52, 0xc8, 0x10, 0xf3, 0x2b, 0x80, 0x90, 0x79, 0xe5,
0x62, 0xf8, 0xea, 0xd2, 0x52, 0x2c, 0x6b, 0x7b };
uint8_t in[] = { 0xbd, 0x33, 0x4f, 0x1d, 0x6e, 0x45, 0xf2, 0x5f, 0xf7, 0x12, 0xa2, 0x14, 0x57, 0x1f, 0xa5, 0xcc };
#elif defined(AES128)
uint8_t key[] = { 0x2b, 0x7e, 0x15, 0x16, 0x28, 0xae, 0xd2, 0xa6, 0xab, 0xf7, 0x15, 0x88, 0x09, 0xcf, 0x4f, 0x3c };
uint8_t in[] = { 0x3a, 0xd7, 0x7b, 0xb4, 0x0d, 0x7a, 0x36, 0x60, 0xa8, 0x9e, 0xca, 0xf3, 0x24, 0x66, 0xef, 0x97 };
#endif
struct AES_ctx ctx;
AES_init_ctx(&ctx, key);
AES_ECB_decrypt(&ctx, in);
// "".join([chr(b) for b in []])
printf("ECB decrypt: \n");
for (int i = 0; i < sizeof(in) / sizeof(in[0]); i++)
{
printf("0x%02x, ", in[i]);
}
printf("\n");
return(0);
}実際にこの結果が正しいかどうかは、以下の Python スクリプトの結果と比較することで確認しました。
from Crypto.Cipher import AES
key = [0x60, 0x3d, 0xeb, 0x10, 0x15, 0xca, 0x71, 0xbe, 0x2b, 0x73, 0xae, 0xf0, 0x85, 0x7d, 0x77, 0x81, 0x1f, 0x35, 0x2c, 0x07, 0x3b, 0x61, 0x08, 0xd7, 0x2d, 0x98, 0x10, 0xa3, 0x09, 0x14, 0xdf, 0xf4]
key = bytes([int(hex(x),0) for x in key])
cipher = AES.new(key, AES.MODE_ECB)
plaintext = b"testtesttesttest"
cipher_text = cipher.encrypt(plaintext)
print("PlainText : ", plaintext)
print("Encrypt : ", ",".join([hex(c) for c in cipher_text]))
print("Decrypt : ", cipher.decrypt(cipher_text))上記のコードを実行すると、カスタムした C プログラムで暗号化した際と同じ結果を得ることができました。
カスタム SBox を使用して暗号化されたデータを復号する
次に、SBox のカスタマイズも試してみます。
SBox は、aes.c にハードコードされています。
Android のネイティブライブラリ関数解析と RC4 と AES の復号を行う【WMCTF 2023】 の問題を思いだして、SBox と Inverse SBox をそれぞれ以下に置き換えます。
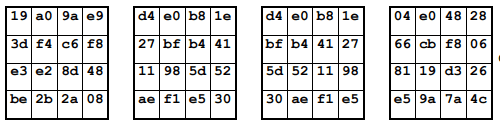
static const uint8_t sbox[256] = {
0x29,0x40,0x57,0x6e,0x85,0x9c,0xb3,0xca,
0xe1,0xf8,0x0f,0x26,0x3d,0x54,0x6b,0x82,
0x99,0xb0,0xc7,0xde,0xf5,0x0c,0x23,0x3a,
0x51,0x68,0x7f,0x96,0xad,0xc4,0xdb,0xf2,
0x09,0x20,0x37,0x4e,0x65,0x7c,0x93,0xaa,
0xc1,0xd8,0xef,0x06,0x1d,0x34,0x4b,0x62,
0x79,0x90,0xa7,0xbe,0xd5,0xec,0x03,0x1a,
0x31,0x48,0x5f,0x76,0x8d,0xa4,0xbb,0xd2,
0xe9,0x00,0x17,0x2e,0x45,0x5c,0x73,0x8a,
0xa1,0xb8,0xcf,0xe6,0xfd,0x14,0x2b,0x42,
0x59,0x70,0x87,0x9e,0xb5,0xcc,0xe3,0xfa,
0x11,0x28,0x3f,0x56,0x6d,0x84,0x9b,0xb2,
0xc9,0xe0,0xf7,0x0e,0x25,0x3c,0x53,0x6a,
0x81,0x98,0xaf,0xc6,0xdd,0xf4,0x0b,0x22,
0x39,0x50,0x67,0x7e,0x95,0xac,0xc3,0xda,
0xf1,0x08,0x1f,0x36,0x4d,0x64,0x7b,0x92,
0xa9,0xc0,0xd7,0xee,0x05,0x1c,0x33,0x4a,
0x61,0x78,0x8f,0xa6,0xbd,0xd4,0xeb,0x02,
0x19,0x30,0x47,0x5e,0x75,0x8c,0xa3,0xba,
0xd1,0xe8,0xff,0x16,0x2d,0x44,0x5b,0x72,
0x89,0xa0,0xb7,0xce,0xe5,0xfc,0x13,0x2a,
0x41,0x58,0x6f,0x86,0x9d,0xb4,0xcb,0xe2,
0xf9,0x10,0x27,0x3e,0x55,0x6c,0x83,0x9a,
0xb1,0xc8,0xdf,0xf6,0x0d,0x24,0x3b,0x52,
0x69,0x80,0x97,0xae,0xc5,0xdc,0xf3,0x0a,
0x21,0x38,0x4f,0x66,0x7d,0x94,0xab,0xc2,
0xd9,0xf0,0x07,0x1e,0x35,0x4c,0x63,0x7a,
0x91,0xa8,0xbf,0xd6,0xed,0x04,0x1b,0x32,
0x49,0x60,0x77,0x8e,0xa5,0xbc,0xd3,0xea,
0x01,0x18,0x2f,0x46,0x5d,0x74,0x8b,0xa2,
0xb9,0xd0,0xe7,0xfe,0x15,0x2c,0x43,0x5a,
0x71,0x88,0x9f,0xb6,0xcd,0xe4,0xfb,0x12 };
#if (defined(CBC) && CBC == 1) || (defined(ECB) && ECB == 1)
static const uint8_t rsbox[256] = {
0x41,0xE8,0x8F,0x36,0xDD,0x84,0x2B,0xD2,
0x79,0x20,0xC7,0x6E,0x15,0xBC,0x63,0x0A,
0xB1,0x58,0xFF,0xA6,0x4D,0xF4,0x9B,0x42,
0xE9,0x90,0x37,0xDE,0x85,0x2C,0xD3,0x7A,
0x21,0xC8,0x6F,0x16,0xBD,0x64,0x0B,0xB2,
0x59,0x00,0xA7,0x4E,0xF5,0x9C,0x43,0xEA,
0x91,0x38,0xDF,0x86,0x2D,0xD4,0x7B,0x22,
0xC9,0x70,0x17,0xBE,0x65,0x0C,0xB3,0x5A,
0x01,0xA8,0x4F,0xF6,0x9D,0x44,0xEB,0x92,
0x39,0xE0,0x87,0x2E,0xD5,0x7C,0x23,0xCA,
0x71,0x18,0xBF,0x66,0x0D,0xB4,0x5B,0x02,
0xA9,0x50,0xF7,0x9E,0x45,0xEC,0x93,0x3A,
0xE1,0x88,0x2F,0xD6,0x7D,0x24,0xCB,0x72,
0x19,0xC0,0x67,0x0E,0xB5,0x5C,0x03,0xAA,
0x51,0xF8,0x9F,0x46,0xED,0x94,0x3B,0xE2,
0x89,0x30,0xD7,0x7E,0x25,0xCC,0x73,0x1A,
0xC1,0x68,0x0F,0xB6,0x5D,0x04,0xAB,0x52,
0xF9,0xA0,0x47,0xEE,0x95,0x3C,0xE3,0x8A,
0x31,0xD8,0x7F,0x26,0xCD,0x74,0x1B,0xC2,
0x69,0x10,0xB7,0x5E,0x05,0xAC,0x53,0xFA,
0xA1,0x48,0xEF,0x96,0x3D,0xE4,0x8B,0x32,
0xD9,0x80,0x27,0xCE,0x75,0x1C,0xC3,0x6A,
0x11,0xB8,0x5F,0x06,0xAD,0x54,0xFB,0xA2,
0x49,0xF0,0x97,0x3E,0xE5,0x8C,0x33,0xDA,
0x81,0x28,0xCF,0x76,0x1D,0xC4,0x6B,0x12,
0xB9,0x60,0x07,0xAE,0x55,0xFC,0xA3,0x4A,
0xF1,0x98,0x3F,0xE6,0x8D,0x34,0xDB,0x82,
0x29,0xD0,0x77,0x1E,0xC5,0x6C,0x13,0xBA,
0x61,0x08,0xAF,0x56,0xFD,0xA4,0x4B,0xF2,
0x99,0x40,0xE7,0x8E,0x35,0xDC,0x83,0x2A,
0xD1,0x78,0x1F,0xC6,0x6D,0x14,0xBB,0x62,
0x09,0xB0,0x57,0xFE,0xA5,0x4C,0xF3,0x9A };
#endif続いて、バイナリから特定したキーと暗号化データを使用して、test.c のコードを以下に置き換えました。
#include <stdio.h>
#include <stdint.h>
#include <string.h>
#include <math.h>
#include <stdlib.h>
#include <time.h>
#include "aes.h"
// test.c にコピーして使う
// SBox をカスタマイズする場合は、aes.c を編集する
// make test で AES 128,192,256 の各パターンをテストできる
int main() {
unsigned char buf[16] = {
0x2B, 0xC8, 0x20, 0x8B, 0x5C, 0x0D, 0xA7, 0x9B, 0x2A, 0x51, 0x3A, 0xD2, 0x71, 0x71, 0xCA, 0x50
};
char *key = malloc(17);
memcpy(key, "Re_1s_eaSy123456", 17);
struct AES_ctx aesCtx;
AES_init_ctx(&aesCtx, (uint8_t*)key);
AES_ECB_decrypt(&aesCtx, buf);
printf("%s\n", buf);
// WMCTF{Re_1s_eaSy_eZ_Rc4_@nd_AES!}
return 0;
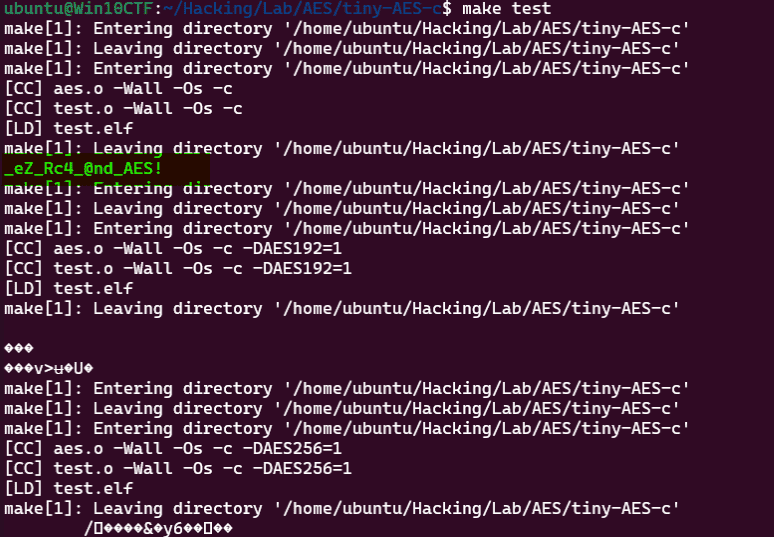
}これで、make test を実行したところ、以下のように AES-128 の復号結果が正しいパスワード文字列 _eZ_Rc4_@nd_AES! になることを確認できました。
デコンパイル結果から AES による暗号化を行う処理を見抜く
ここまでで、なんとなく AES の Cipher 内で行われる処理の雰囲気をつかむことができたような気がします。
今まではデコンパイル結果からどうやって AES かどうかを特定すればええんやという気持ちでしたが、少し AES の実装に対する解像度が上がったことで、以前よりはスムーズに見抜けるようになりそうな気がします。
というわけで、tiny-AES-c の IDA でのデコンパイル結果を見てみます。
- tiny-AES-c の cipher 関数のデコンパイル結果
__int64 __fastcall Cipher(__int64 a1, __int64 a2)
{
int v2; // r13d
int v3; // r14d
unsigned int v4; // ebx
_BYTE *v5; // r10
__int64 v6; // r11
_BYTE *v7; // rcx
unsigned __int8 *v8; // rdx
unsigned __int8 *v9; // rax
__int64 v10; // rsi
__int64 v11; // r8
char v12; // al
char v13; // dl
char v14; // al
char v15; // dl
char v16; // al
char v17; // dl
char v18; // al
_BYTE *v19; // rcx
int v20; // r12d
char v21; // al
int v22; // r12d
char v23; // r8
__int64 v24; // rcx
__int64 v25; // rdx
__int64 v26; // rcx
__int64 v27; // rdx
unsigned __int8 v28; // r8
__int64 v29; // rcx
__int64 v30; // rdx
__int64 v31; // r10
__int64 v32; // r11
_BYTE *v33; // r9
__int64 v34; // rdi
v4 = 1;
AddRoundKey(0LL, a1, a2);
while ( 1 )
{
v7 = v5;
v8 = v5;
do
{
v9 = v8;
LODWORD(v10) = 0;
do
{
v11 = *v9;
v10 = (unsigned int)(v10 + 1);
v9 += 4;
*(v9 - 4) = sbox[v11];
}
while ( (_BYTE)v10 != 4 );
++v8;
}
while ( v5 + 4 != v8 );
v12 = v5[1];
v5[1] = v5[5];
v5[5] = v5[9];
v13 = v5[13];
v5[13] = v12;
v14 = v5[2];
v5[9] = v13;
v15 = v5[10];
v5[10] = v14;
v16 = v5[6];
v5[2] = v15;
v17 = v5[14];
v5[14] = v16;
v18 = v5[3];
v5[6] = v17;
v5[3] = v5[15];
v5[15] = v5[11];
LOBYTE(v8) = v5[7];
v5[7] = v18;
v5[11] = (_BYTE)v8;
if ( v4 == 10 )
break;
do
{
LOBYTE(v11) = *v7;
LOBYTE(v3) = v7[1];
v19 = v7 + 4;
LOBYTE(v2) = *(v19 - 2);
LOBYTE(v10) = *(v19 - 1);
v20 = v3 ^ v11;
v21 = xtime((unsigned __int8)(v3 ^ v11), v10, v8, v19);
v22 = v10 ^ v2 ^ v20;
*(_BYTE *)(v24 - 4) = v22 ^ v23 ^ v21;
v3 ^= v22 ^ xtime((unsigned __int8)(v2 ^ v3), v10, v25, v24);
*(_BYTE *)(v26 - 3) = v3;
v2 ^= v22 ^ xtime((unsigned __int8)(v10 ^ v2), v10, v27, v26);
*(_BYTE *)(v29 - 2) = v2;
v10 = v22 ^ (unsigned int)xtime(v28, v10, v30, v29) ^ (unsigned int)v10;
*(v7 - 1) = v10;
}
while ( v33 != v7 );
v34 = v4++;
AddRoundKey(v34, v31, v32);
}
return AddRoundKey(10LL, v5, v6);
}AddRoundKey のシンボルが無かったらこれで AES を使っているとすぐに判断するのは結構厳しいような気がしますね。
やるとしたらデータセクションから SBox の定義を見つけて、そこを参照している関数から最初の State 初期化の処理を見つけるとか、やたらと 4 ブロックに分割している処理を特定するとかになるんでしょうか?
このあたりはもう少し精進が必要そうです。
まとめ
暗号も引き続き勉強していきます。
Rev 力上げたい。